|
|
угол p - a. Итак, на отрезке [ 0 ; 2p
] при ![]() < 1 уравнение
< 1 уравнение ![]() имеет
два решения - a и p - a.
имеет
два решения - a и p - a.
Определение. Пусть число ![]() по модулю не
превосходит единицы. Арксинусом числа
по модулю не
превосходит единицы. Арксинусом числа ![]() называется
угол
называется
угол ![]() , лежащий в пределах от -
, лежащий в пределах от -![]() до +
до +![]() , синус
которого равен
, синус
которого равен ![]() . Обозначается
. Обозначается ![]() .
.
Из рис.
26. видим, что 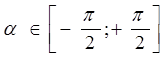 , поэтому
, поэтому ![]() .
Таким образом, все решения уравнения
.
Таким образом, все решения уравнения ![]() при
при ![]() <
1 получаются по формулам:
<
1 получаются по формулам:
![]() ,
, ![]() ,
, ![]() или в
виде одной формулы
или в
виде одной формулы
![]() ,
, ![]() . (1)
. (1)
При ![]() = 1 (из рис. 26.) решениями будут
= 1 (из рис. 26.) решениями будут
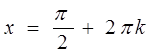
при ![]() = 1 или
= 1 или
![]()
при ![]() = -1.
= -1.
Так как 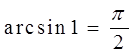 , то из (1) имеем
, то из (1) имеем
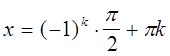
или
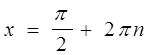 , при
, при ![]() ,
, ![]()
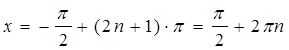 , при
, при ![]() ,
, ![]() .
.
Аналогично, из 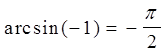 по формуле (1) получим
по формуле (1) получим
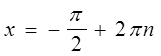 ,
, ![]() .
.
Итак, формула
![]() ,
, ![]()
даёт решения
уравнения ![]() при
при ![]() £ 1.
£ 1.
2) Рассмотрим
уравнение ![]() . Так как область значений
косинуса - отрезок [ -1 ; 1 ], то при
. Так как область значений
косинуса - отрезок [ -1 ; 1 ], то при ![]() > 1 уравнение решений не имеет; если
> 1 уравнение решений не имеет; если ![]() £
1, то решений бесконечно много ( рис. 27).
£
1, то решений бесконечно много ( рис. 27).
|
|
Так как косинус имеет
наименьший положительный период 2p, то
достаточно найти все решения в пределах одного периода. По графику видно, что
при ![]() <
1 на отрезке [ -p ; p ] есть два угла, косинус которых равен
<
1 на отрезке [ -p ; p ] есть два угла, косинус которых равен ![]() . Пусть на [
0 ; p ]
решением будет угол a, т. е.
. Пусть на [
0 ; p ]
решением будет угол a, т. е. ![]() .Ввиду чётности косинуса на [ -p
; 0 ] решением будет угол (-a).
.Ввиду чётности косинуса на [ -p
; 0 ] решением будет угол (-a).
Итак, на [ -p
; p ]
уравнение ![]() при
при ![]() < 1 имеет два решения a и -a.
< 1 имеет два решения a и -a.
Определение. Пусть ![]() - число, по модулю не превосходящее
единицы. Арккосинусом числа
- число, по модулю не превосходящее
единицы. Арккосинусом числа ![]() называется угол
называется угол ![]() , лежащий в пределах от 0 до p, косинус которого равен
, лежащий в пределах от 0 до p, косинус которого равен ![]() . Обозначается
. Обозначается ![]() .
.
Так как a Î [ 0 ; p
], то ![]() .Таким
образом все решения уравнения
.Таким
образом все решения уравнения
![]()
исчерпываются двумя сериями:
![]() ;
; ![]() ,
, ![]() .
.
Эти серии обычно записываются в виде одной формулы:
![]() ,
, ![]() .
(2)
.
(2)
Если ![]() =
1, то (из рис. 27) решениями будут
=
1, то (из рис. 27) решениями будут
![]() ,
, ![]()
при ![]() = 1 и
= 1 и
![]() ,
, ![]() .
.
Поскольку ![]() ,
то при
,
то при ![]() = -1 из (2) получаем
= -1 из (2) получаем
![]() ,
, ![]() .
.
Итак, формула
![]() ,
, ![]() .
.
Даёт решения уравнения ![]() при
при ![]() £ 1.
£ 1.
3) Рассмотрим
уравнение ![]() . Область значений тангенса - все
действительные числа. Поэтому уравнение
. Область значений тангенса - все
действительные числа. Поэтому уравнение ![]() имеет
решение при любом
имеет
решение при любом![]() . Наименьший положительный
период тангенса - p. В пределах этого
периода тангенс принимает каждое значение ровно один раз. Построим на одном
чертеже графики функций
. Наименьший положительный
период тангенса - p. В пределах этого
периода тангенс принимает каждое значение ровно один раз. Построим на одном
чертеже графики функций ![]() и
и ![]() (рис. 28.).
(рис. 28.).
|
|
Определение. Арктангенсом
числа ![]() называется угол
называется угол 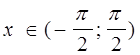 ,
тангенс которого равен
,
тангенс которого равен ![]() . Обозначается
. Обозначается ![]() .
.
На (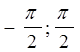 )
уравнение
)
уравнение
![]()
имеет одно решение
![]() .
.
Учитывая периодичность функции
получим, что все решения уравнения ![]() описываются
формулой
описываются
формулой
![]() ,
, ![]() .
.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, КОТОРЫЕ СВОДЯТСЯ К ПРОСТЕЙШИМ.
Уравнения вида
![]() ,
, ![]() ,
, ![]() , где
, где ![]() -
заданная функция, сводятся к простейшим соответствующими подстановками
-
заданная функция, сводятся к простейшим соответствующими подстановками
![]() ,
, ![]() ,
, ![]() .
.
Уравнения, однородные
относительно ![]() и
и ![]() ,
например, вида
,
например, вида
![]() ,
, ![]()
или вида
![]() ,
, ![]()
решаются делением обеих частей на
![]() (или
(или ![]() ), или
соответственно на
), или
соответственно на ![]() ( или
( или ![]() )
и последующей подстановкой
)
и последующей подстановкой ![]() . Потеря корней не
происходит и посторонние не появляются, так как
. Потеря корней не
происходит и посторонние не появляются, так как ![]() и
и ![]() не могут одновременно равняться нулю.
не могут одновременно равняться нулю.
Уравнения
![]()
сводятся к однородному заменой
![]() .
.
После преобразований получаем уравнение
![]() , которое равносильно исходному.
, которое равносильно исходному.
В общем случае уравнение вида
![]() , где
, где ![]() -
функция, удовлетворяющая условию
-
функция, удовлетворяющая условию
![]()
для некоторого натурального числа
n, решается делением обеих частей на ![]() или
или ![]() .
.
Уравнение
![]() ,
, ![]()
можно решать делением обеих
частей на ![]() и введением вспомогательного угла j по формулам
и введением вспомогательного угла j по формулам
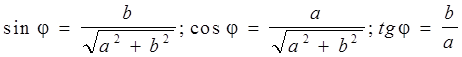 .
.
Тогда уравнение ![]() примет вид
примет вид
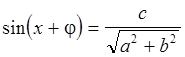 , где
, где 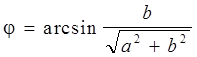 или
или
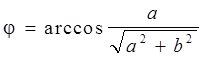 .
.
Уравнение вида
![]()
решается подстановкой
![]() .
.
Тогда
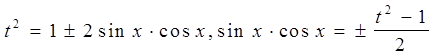 .
.
В результате получаем уравнение
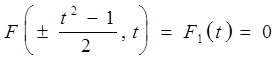 .
.
Уравнение, содержащее
функции ![]()
![]() в чётных степенях можно
упростить используя формулы понижения степени:
в чётных степенях можно
упростить используя формулы понижения степени:
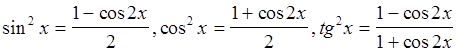 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.