Определение и свойства функции y=sin x и её график. Определение и свойства функции y=cos x и её график. Определение и свойства функции y=tgx и её график. Зависимость между тригонометрическими функциями одного и того же аргумента

ОПРЕДЕЛЕНИЕ И СВОЙСТВА ФУНКЦИИ  И ЕЁ ГРАФИК.

     Определение. Окружность радиуса 1 с центром в начале координат называют единичной окружностью.

Рассмотрим точку  - образ точки  при повороте вокруг начала координат на угол , измеренный в радианах (рис.18).

Синусом числа (обозначение ) называется ордината точки . Таким образом, . Сопоставляя каждому действительному числу  его синус, получим функцию .

Свойства функции .

1.  Область определения - все действительные числа, т. е. . Действительно, угол может меняться от  -¥ до +¥ и при каждом конкретном его значении будет однозначно определена точка на единичной окружности, ордината которой и есть синус данного угла.

2.  Область значенийфункции - отрезок [ -1 ; 1 ], т. е. [ -1 ; 1 ]. Действительно, при любом ордината соответствующей точки на единичной окружности удовлетворяет неравенству  -1 £  £ 1 (рис.18).

3.  Функция  нечётна, так как ординаты точек и противоположны (рис.18). Это означает, что .Следовательно, график симметричен относительно начала координат.

4.  Функция  периодическая с периодами ( ), так как точки, полученные при повороте на угол и  +  совпадают. Докажем, что наименьший положительный период равен 2p. Пусть  > 0 - наименьший положительный период. Тогда   при любом . В частности, при  = 0, имеем , т. е. , откуда следует, что  может принимать значения  p, 2p и т. д. Но если   =  p, то равенство  должно выполняться при всех . Полагая = , приходим к противоречию, т. к. 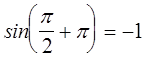, а 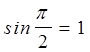. Таким образом,  =  2p - наименьший положительный период. Поэтому для построения графика функции достаточно провести построения на отрезке [ 0 ; 2p ], а затем полученный график параллельно перенести на ( ) вправо и влево вдоль оси .

5.  Точки пересечения с осями координат. С осью : если = 0, то         . С осью  (нули функции): = 0 , откуда = ,  

( в концах горизонтального диаметра ординаты равны 0).

6.  Промежутки знакопостоянства. Так как ординаты точек верхней полуплоскости положительны, то для углов, находящихся в первой и второй четвертях, > 0. Поскольку точки нижней полуплоскости имеют отрицательные ординаты,  то  для  углов,  находящихся   в   третьей   и   четвёртой   четвертях,  < 0. Таким образом, > 0 при всех  , ,  < 0 при всех , .

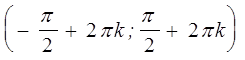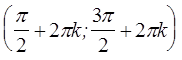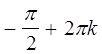7.  Промежутки монотонности и экстремумы. Из рис. 18 нетрудно заметить, что при изменении  от   до  значение возрастает от -1 до 1. Следовательно, на промежутках , , функция возрастает. При изменении от   до значение уменьшается от -1 до 1. Следовательно, на промежутке , , функция  убывает. Тогда в точках  функция имеет минимальные значения  -1, а в точках 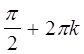,  - максимальные значения 1.

8.  График функции называется синусоидой (рис.19).

ОПРЕДЕЛЕНИЕ И СВОЙСТВА ФУНКЦИИ  И ЕЁ ГРАФИК.

Определение. Рассмотрим единичную окружность (рис. 20).

Пусть точка  - образ точки  при повороте радиус-векторавокруг начала координат на угол , измеренный в радианах (рис.20).

Косинусом числа   (обозначение ) называется абсцисса точки . Таким образом, . Сопоставляя каждому действительному числу  его косинус, получим функцию .

                                              Свойства функции .

1.  Область определения - все действительные числа, т. е. . Действительно, угол может изменяться от  -¥ до +¥ и при каждом конкретном его значении будет однозначно определена точка на единичной окружности, абсцисса которой и есть косинус данного угла.

2.  Область значенийфункции  - отрезок [ -1 ; 1 ], т. е.  = [ -1 ; 1 ]. Действительно, при любом абсцисса соответствующей точки на единичной окружности удовлетворяет неравенству   -1 £  £ 1.

3.  Функция  чётная, так как абсцисса точки , соответствующей углу , равна абсциссе точки , соответствующей углу  -(рис.20). Следовательно и график функции симметричен относительно оси .

4. Функция периодическая с периодами ( ), так как  образы точки при повороте  на угол  и +  совпадают. Докажем, что наименьший период равен 2p. Пусть  > 0 - наименьший положительный период. Тогда   при  любом  .  Полагая  здесь , получаем . Но наименьшее положительное , для которого косинус равен единице есть 2p.

Для построения графика функции достаточно провести построения на отрезке [ 0 ; 2p ], а затем полученный график параллельно перенести на ( ) вправо и влево вдоль оси .

5.  Точки пересечения с осями координат. С осью : если = 0, то    . С осью  (нули функции): =0, откуда ,

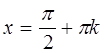 (в концах вертикального диаметра абсциссы равны 0).

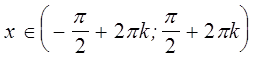6.  Промежутки знакопостоянства. Так как абсциссы точек правой полуплоскости положительны, то для углов, находящихся в первой и четвёртой  четвертях, > 0. Поскольку точки левой полуплоскости имеют отрицательные абсциссы, то для углов, находящихся во второй и третьей четвертях, < 0. Таким образом > 0 при всех , ; < 0 при всех , .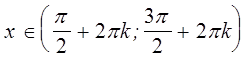

8.  Промежутки монотонности и экстремумы. Из рис. 20 нетрудно заметить, что при изменении  от   до  значение возрастает от -1 до 1. Следовательно, на промежутках , , функция возрастает. При изменении от   до значение уменьшается от 1 до -1. Следовательно, на промежутке , , функция убывает. Тогда в точках  функция имеет минимальные значения  -1, а в точках ,  - максимальные значения 1.

8.  График функции  называетсякосинусоидой(рис.21).

 СВОЙСТВА ФУНКЦИИ  И ЕЁ ГРАФИК.

Тангенсом числаa называют отношение синуса этого числа к косинусу того же числа: