Определение и свойства функции y=sin x и её график. Определение и свойства функции y=cos x и её график. Определение и свойства функции y=tgx и её график. Зависимость между тригонометрическими функциями одного и того же аргумента, страница 3

Однако при решении примеров и задач часто необходимо вычислять и значения тригонометрических функций углов, больших . Выведем формулы, позволяющие свести такие вычисления к значениям острых углов. Такие формулы называются формулами приведения.

Так как  - наименьший положительный период для синуса и косинуса, то нахождение значений этих функций сводится к вычислению их значений от аргумента, в пределах от до . Из формул сложения следует, что

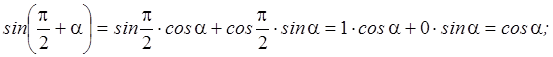
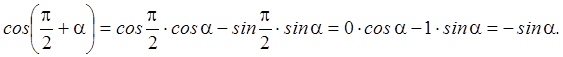
Таким образом

.

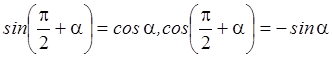Для тангенса и котангенса

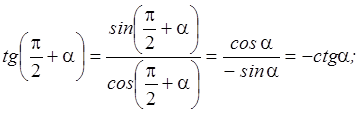
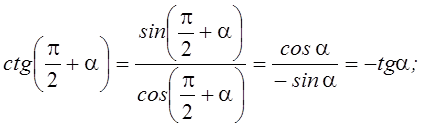
т. е.

.

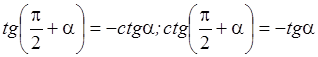Аналогично можно получить формулы приведения для углов .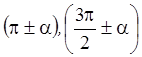

В результате применения этих формул можно составить следующую таблицу

Функция

Функцию косинус называют кофункцией функции синус и обратно. В таком отношении находятся и функции тангенс и котангенс. Используя понятие кофункции, приведём два правила для запоминания формул приведения.

1.  Если в формуле приведения острый угол  прибавляется к углам  и  или вычитается из них, то функция меняет своё название на кофункцию. Знак берётся тот, который имеет первоначальная функция в четверти всего угла.

2.  Если в формуле приведения острый угол  прибавляется к углам  и , или вычитается из них, то функция не меняет своего названия. Знак определяется аналогично правилу 1.

В случае когда угол превосходит используется свойство периодичности тригонометрических функций.

Пример 1. Найти .

Решение. 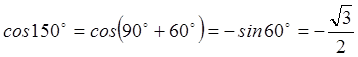. Знак (-) взят потому что угол находится во второй четверти, в которой косинус отрицателен.

СИНУС, КОСИНУС, ТАНГЕНС ДВОЙНОГО АРГУМЕНТА.

Полагая в формулах:

 

 

.

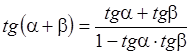угол b равный a, получим соответственно формулы удвоения:

1) ,

2) ,

3) .

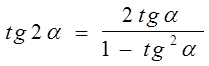Доказательство.

1) .

2) .

3) .

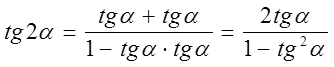СИНУС, КОСИНУС, ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА.

Рассмотрим формулу .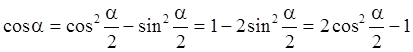

Из первого равенства 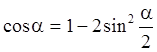  следует 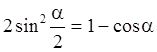 . Откуда

.

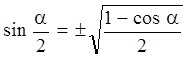Из второго равенства 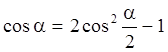 следует 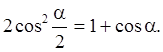Откуда

.

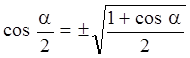Теперь .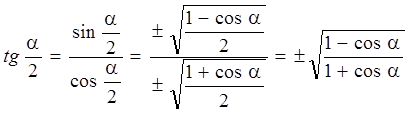

ПРЕОБРАЗОВАНИЕ В ПРОИЗВЕДЕНИЕ СУММ , , .

1)

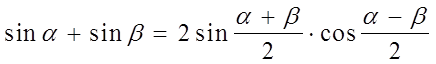
Доказательство. Воспользуемся тождествами:

 ,       .

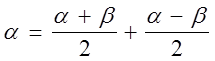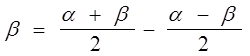Тогда

.

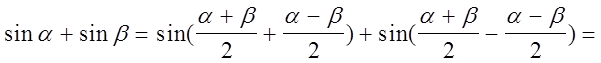
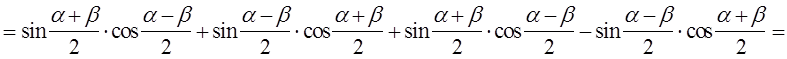
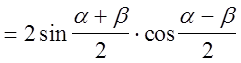2) .

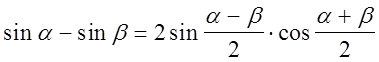Доказательство.

.

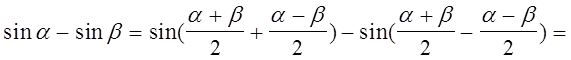
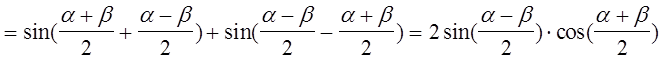3) .

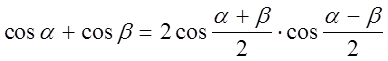Доказательство.

= .

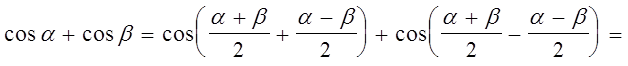
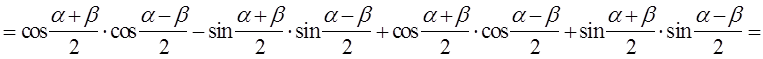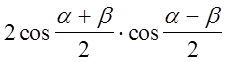4)   .

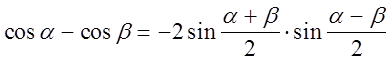Доказательство.

.

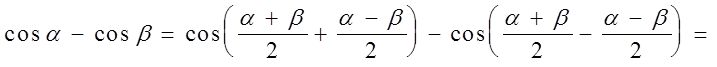
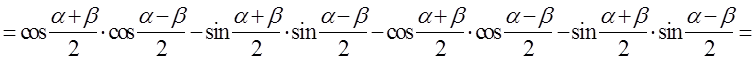
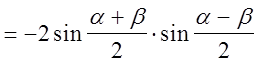5) .

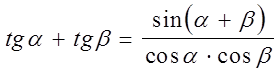Доказательство.

.

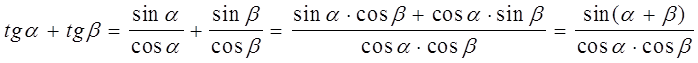6) .

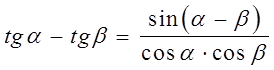Доказательство.

.

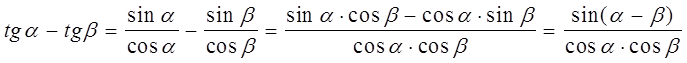РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ВИДА , , .

1) Рассмотрим уравнение . Так как областью значений синуса является отрезок [ -1 ; 1 ], то это уравнение не имеет решений при > 1. Пусть теперь £ 1. Построим на одном чертеже графики  и  (рис. 25).

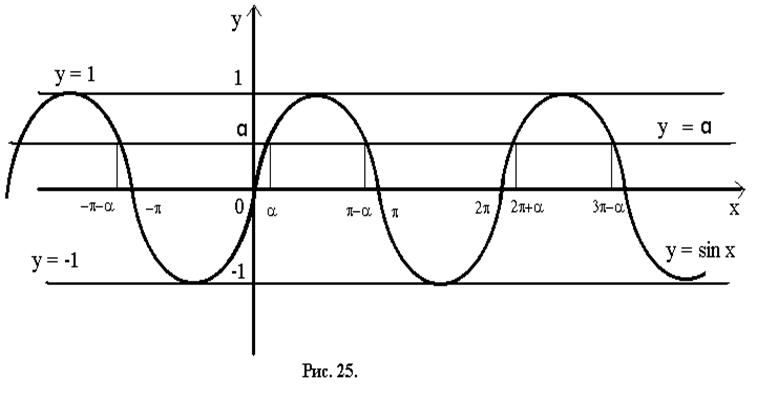
Прямая пересечёт синусоиду бесконечно много раз. Это означает, что уравнение имеет бесконечно много корней. Так как синус имеет наименьший положительный период 2p, то достаточно найти все решения в пределах одного периода. По графику видно, что при < 1 на отрезке [ 0 ; 2p ] есть два угла, синус которых равен .

Рассмотрим единичную окружность (рис. 26). Значению  синуса на [ 0 ; 2p ] соответствуют две точки NиR. Пусть точке Nсоответствует угол a. Точке R соответствует Ð ROK. Но Ð ROK = p - Ð ROL. Нетрудно заметить, что D RLO= D NKO ( OR= ON -радиус, NK= RL = , Ð RLO= Ð NKO = 90°). Тогда Ð ROL = a. Следовательно, точке R соответствует