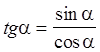 .
.
|
|
Дадим геометрическую
интерпретацию этого определения. Рассмотрим прямую ![]() ,
проходящую через точку
,
проходящую через точку ![]() единичной окружности (рис. 22).
Пусть для определённости
единичной окружности (рис. 22).
Пусть для определённости 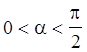 . Точку пересечения этой
прямой с
. Точку пересечения этой
прямой с ![]() обозначим
обозначим ![]() . Из подобия
треугольников
. Из подобия
треугольников ![]() получаем:
получаем: 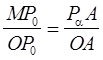 . Так как
. Так как ![]() ,
, ![]() , то
, то
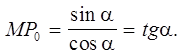
Таким образом, ордината
точки ![]() есть тангенс угла
есть тангенс угла ![]() ,
поэтому прямую
,
поэтому прямую ![]() называют линией тангенсов.
называют линией тангенсов.
Сопоставляя каждому
действительному числу 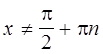 ,
,![]() его тангенс, получим функцию
его тангенс, получим функцию ![]() . Рассмотрим свойства функции более подробно.
. Рассмотрим свойства функции более подробно.
1. Функция ![]() определена при всех действительных
определена при всех действительных ![]() , кроме
, кроме 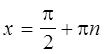 , где
, где ![]() .
.
2. Область значений функции ![]() - вся числовая ось.
- вся числовая ось. ![]() . Следовательно, функция
. Следовательно, функция ![]() - функция неограниченная.
- функция неограниченная.
3. Тангенс - нечётная функция, так как
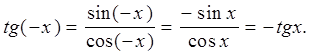
Её график симметричен относительно начала координат.
4. Тангенс - периодическая
функция с наименьшим положительным периодом ![]() .
.
5. ![]() при всех
при всех
![]()
6. ![]() при
всех
при
всех 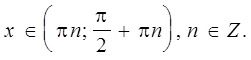
7. ![]() при всех
при всех
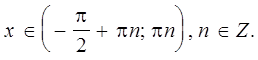
8. Функция ![]() экстремумов не имеет.
экстремумов не имеет.
9. Функция ![]() возрастает в каждом промежутке
возрастает в каждом промежутке 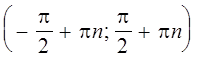 ,
, ![]() .
.
|
|
График
функции ![]() называетсятангенсоидой
(рис. 23).
называетсятангенсоидой
(рис. 23).
ЗАВИСИМОСТЬ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ ОДНОГО И ТОГО ЖЕ АРГУМЕНТА.
Каждую тригонометрическую функцию некоторого
аргумента можно выразить через любую другую тригонометрическую функцию одного и
того же аргумента. Действительно, из основного тригонометрического тождества ![]() следует, что
следует, что ![]() ,
, ![]() , откуда
, откуда ![]() ,
, ![]() .
.
Предположив, что ![]() ,
разделим почленно основное тождество на
,
разделим почленно основное тождество на ![]() , получим
, получим
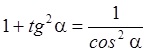 .
.
Предположив теперь, что ![]() ,
разделим почленно основное тождество на
,
разделим почленно основное тождество на ![]() , получим
, получим
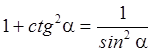 . Причём первая формула верна при
. Причём первая формула верна при 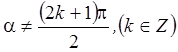 , вторая при
, вторая при ![]() .
.
Кроме того 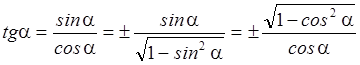 ,
,
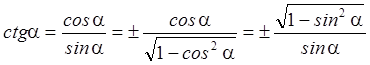 .
.
Учитывая определения тангенса и котангенса,
получаем 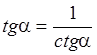 ,
, 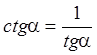 ,
, ![]() . Из равенства
. Из равенства 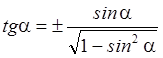 ,
выразим
,
выразим 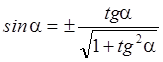 . Из равенства
. Из равенства 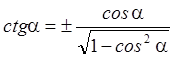 ,
получаем
,
получаем 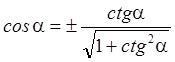 .
.
СИНУС, КОСИНУС, ТАНГЕНС СУММЫ (РАЗНОСТИ) ДВУХ АРГУМЕНТОВ.
Теорема. Косинус разности двух углов равен произведению косинусов этих углов, сложенному с произведением синусов:
![]() (1)
(1)
|
|
Доказательство. Построим
углы a и b
с помощью единичной окружности, т.е. точки ![]() и
и ![]() такие, что векторы
такие, что векторы ![]() и
и
![]() образуют углы a и b с положительным
направлением оси абсцисс. Угол между векторами
образуют углы a и b с положительным
направлением оси абсцисс. Угол между векторами ![]() и
и ![]() равен a
- b (рис. 24).
равен a
- b (рис. 24).
Вычислим скалярное
произведение этих векторов учитывая, что |![]() | =
|
| =
|![]() | = 1.
| = 1.
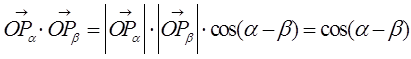 .
.
Теперь вычислим это же скалярное произведение с помощью координат:
![]() ×
×![]() =
= ![]() .
.
Сравнивая результаты вычислений, получаем требуемую формулу
![]() .
.
Теорема доказана.
Формула (1) называется формулой косинуса разностидвух аргументов. Остальные формулы получаются как следствие этой теоремы.
Косинус суммы.
![]() .
.
Получили
![]() . (2)
. (2)
Синус суммы.
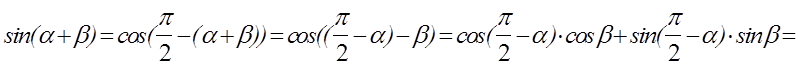
![]() .
.
Получили
![]() . (3)
. (3)
Синус разности.
![]() .
.
Окончательно
![]() . (4)
. (4)
Тангенс суммы.
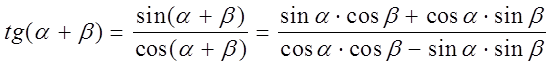
Разделив числитель и знаменатель
этой дроби на произведение ![]() , получим
, получим
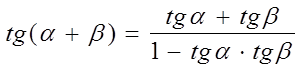 . (5)
. (5)
Тангенс разности.
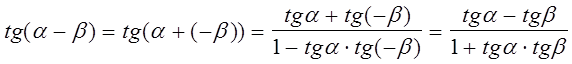 .
.
Получили
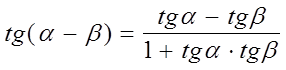 . (6)
. (6)
Формулы (1) - (6) называются формулами сложения.
ФОРМУЛЫ ПРИВЕДЕНИЯ.
Значения тригонометрических функций некоторых острых углов даны в следующей таблице:
|
Функция |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.