Министерство образования Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«Комсомольский-на-Амуре государственный технический Университет»
Кафедра " Машины и технология литейного производства "
ИЗУЧЕНИЕ ЗАВИСИМОСТИ ТЕПЛОПРОВОДНОСТИ
СЫПУЧИХ МАТЕРИАЛОВ ОТ ТЕМПЕРАТУРЫ
Методические указания к лабораторной работе 2
по курсу «Теория тепловых процессов»
Комсомольск-на-Амуре 2003
УДК 621.745.5: 669.1
Изучение зависимости теплопроводности сыпучих материалов от температуры: Методические указания к лабораторной работе 2 / Сост. Б.М. Соболев. - Комсомольск-на-Амуре: Комсомольский-на-Амуре гос. техн. ун-т, 2003. - 10 с.
Описана конструкция лабораторной установки, Приведена методика проведения экспериментов и обработки результатов по определению теплопроводности сыпучих материалов. Предназначена для студентов специальностей 120300, 551800, 110600 дневной и заочной форм обучения.
Печатается по постановлению редакционно-издательского совета Комсомольского-на-Амуре государственного технического университета.
Согласовано с отделом стандартизации.
Цель работы: Изучить методику экспериментального определения теплофизических характеристик материалов, механизм передачи тепла в пористых телах.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
Изучение теплофизических характеристик различных материалов позволяет широко использовать экспериментальные данные в проектировании промышленных установок, применяемых при плавке сплавов, термообработке отливок, сушке исходных формовочных материалов, а также в расчетах процессов теплообмена при охлаждении отливок в форме.
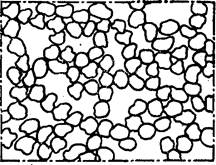
Наблюдения различных зернистых и связанных материалов природного и искусственного происхождения с помощью стереомикроскопа позволяет изобразить на плоскости их внутреннее строение, как показано на рис.1.

а) б)
в). г). д).
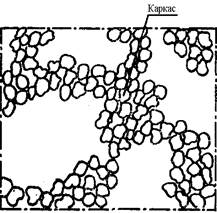
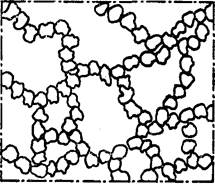
Рис.1. Структура свободной засыпки зерен при различной пористости m2 : а – 0,3< m2 < 0,5; б - m2 » 0,7; в - реальный высокопористый материал. г - цепочная структура; д - трубки тока в каркасе зернистой структуры.
Видно, что структура таких материалов состоит из «каркаса» (рис.1,в), образованного хаотической, но относительно плотной кладкой постоянно контактирующих зерен, которые называются структурой 1-го порядка, и пространственной сети более крупных пустот, пронизывающих каркас и образующих совместно с ним структуру 2-го порядка с взаимопроникающими компонентами. Если частицы каркаса сами являются пористыми (дробленый туф), то саму пористую частицу согласно принятой классификации следует отнести к структуре нулевого порядка, а система в целом будет иметь структуру 3-го порядка. Зернистый материал можно представить в виде полиструктурной системы, сохраняющей устойчивость и изотропность во всем диапазоне изменения пористости m2. m2=V2/V, или m2=1-rн / r1 , где V2 – объем второй компоненты в элементарной ячейке; V- объем элементарной ячейки; rн – насыпная плотность ячейки; r1- плотность вещества зерен.
При свободной засыпке зерна с размером d > 0,2 мм, образуют плотную хаотическую упаковку отдельных частиц с пористостью 0,35 <m2 < 0,45(а). При этом структура засыпки выглядит однородной. При m2 = 0,4 в засыпке можно заметить отдельные участки с возникающей пространственной сетью более крупных пустот (б). Для засыпок мелких частиц (d<0,1 мм) характерна более высокая общая пористость 0,5 < m2< 0,98 (б, в).
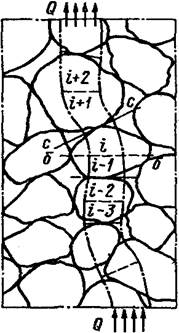
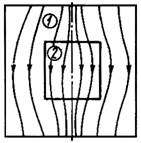
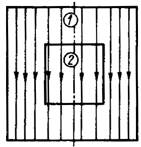
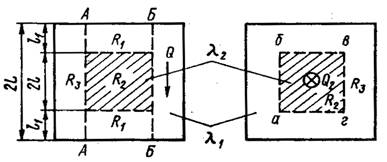
Расчет теплопроводности зернистых структур связан с созданием упрощенной модели передачи тепла в пористом слое. В реальных зернистых структурах тепловые потоки распространяются по пути наименьшего теплового сопротивления (см. рис. 1 д). Рассмотрим приближенный метод расчета обобщенной проводимости для определения эффективной теплопроводности пространственной элементарной ячейки в виде кубов с общим центром и параллельными гранями рис.2.
а) б) в) г)
д) е) ж) з)
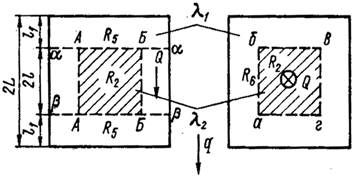
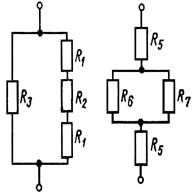
Рис. 2. К расчету проводимости элементарной ячейки: а, б—реальный и упрощенный характер линий тока в ячейке; в, г — дробление элементарной ячейки адиабатными плоскостями (две проекции); ж, з — соединение тепловых сопротивлений частей ячейки при дроблении адиабатами и изотермами
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.