Рис 3. Схема восьмой части элементарной ячейки с взаимопроникающими компонентами
Сущность метода состоит в том, что криволинейный характер линий тока (рис. 2, а) заменяется прямолинейным (рис. 2,6), что упрощает математическое описание исследуемых процессов.
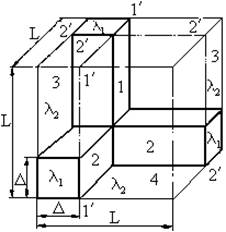
Для линеаризации потока в элементарной ячейке производится дробление ее системой вспомогательных адиабатных или изотермических поверхностей (или их комбинацией), определенным образом ориентированных относительно общего направления потока. На рис. 2, в, г показано в двух проекциях дробление элементарной ячейки вспомогательными адиабатными поверхностями А—А, Б—Б, абвг, что позволяет по простейшим формулам для плоских стенок вычислить тепловые сопротивления отдельных частей ячейки:
R1= l1/ (S1l1) =(L-l)/(4l2l1); R2=2l/(S2l2); R3=2L/ (S3l1), (1.12)
где l1, 2l, 2L — длина пути теплового потока в различных частях ячейки; S1, S2, S3— площади поперечного сечения частей ячейки; l1 , l2 – коэффициенты теплопроводности материала первой и второй компоненты. Схема соединения этих сопротивлений представлена на рис. 2, ж, з, с ее помощью вычисляют общее сопротивление Rвсей ячейки:
R=(2R1+R2)R3/(2R1+R2+R3) (1.13)
Это сопротивление можно представить также в другом виде, используя понятие эффективного коэффициента теплопроводности lвсей ячейки:
R=2L/l S=1/2lL (1.14)
Из формул (1.12) — (1.14) следует, что эффективная теплопроводность
l=(1/2L)(2R1+R2+R3)/ (2R1+R2)R3 (1.15)
На основании формул (1.12) и (1.15) приближенное аналитическое выражение для эффективной теплопроводности структуры с замкнутыми включениями кубической формы имеет следующий вид:
l/l1=[u-(u-1)(1-m22/3)m21/3] / [u- m21/3 (u-1)], где u=l2 / l1 (1.16)
Перенос тепла в порах большинства материалов осуществляется за счет столкновений молекул и излучения. Конвективный перенос тепла, как правило, отсутствует. Однако в определенных условиях (сжатый газ, большой перепад температур в толще высокопористого материала) необходимо оценивать возможность конвективного переноса тепла в пористом слое. Молекулярный перенос тепла в порах осуществляется за счет обмена кинетической энергией при столкновениях движущихся молекул между собой и с поверхностью твердой или жидкой компоненты, ограничивающей поры (поверхность зерен, волокон, жидкости). Без учета конвективного переноса тепла теплопроводность компоненты в порах равна
l2=lм+lл=(lг/(1+B/(H`d ))+4eпрsT3`d, (1.17)
где lм– молекулярная теплопроводность газа в порах ; lл – лучистая составляющая коэффициента теплопроводности; lг- теплопроводность газа в неограниченном пространстве при атмосферном давленииH0 и температуре Т; H- давление в порах; B=4k/(k+1)((2-a)/a)L0H0Pr-1, здесь k-показатель адиабаты; а – коэффициент аккомодации газа на стенках поры; L0 – средняя длина пробега молекул при давлении H0; eпр - приведенный коэффициент взаимного излучения; s - постоянная Стефана-Больцмана (s=5,67 .10-8 Вт/(м2К4));`d - средний линейный размер поры; Pr - критерий Прандтля.
Коэффициент аккомодации газа на стенках поры определяет соотношение масс молекул газа M1 и стенки M2 при множественном столкновении:
a=(1-(M12+M22)/ (M1+M2)2)p, (1.18)
где p – число соударений молекул газа с твердой поверхностью (3<p<4).
Лабораторные методы определения коэффициента теплопроводности многочисленны. Конструктивное многообразие установок зависит от характера материала и уровня температур, в пределах которых проводится исследование. Известные методы принципиально делятся на 2 типа: стационарные и нестационарные.
В данной работе используется метод стационарного теплового потока. Все методы стационарного теплового потока опираются на известные решения задач о тепловом потоке через плоскую, цилиндрическую и сферическую стенки.
В свою очередь методы стационарного теплового потока делятся на абсолютные и относительные. В абсолютных методах на испытательной установке через испытуемый материал проходит весь тепловой поток. Тепло вводится с помощью электрических нагревателей и учитывается по электрическим приборам.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.