Одношаговый итерационный метод с Чебышевскими параметрами

Решение систем линейных алгебраических уравнений методом простой итерации.

Выполнил: студент 2 курса ММФ

Гр. 3112      Кутумов А.А.

Преподаватель: Махоткин О.А.

13.05. 2005 г.

Одношаговый итерационный метод с Чебышевскими параметрами.

Итак, ставится задача нахождения решения уравнения Ах=b, где А – постоянная матрица, b – известный столбец свободных коэффициентов, а х – столбец неизвестных. Предлагается использовать одношаговый итерационный метод с постоянным параметром. Использование постоянного параметра  существенно уменьшает объем вычислений на каждом шаге. Все необходимые алгоритмы и основная теорема приведены  в нижеследующей таблице:

Замечание: данная теорема верна для любого конечного m (в частности и для m=1).

Программная реализация:

Начальный вектор выбирается случайным образом. При итерационном шаге вычисляется следующее приближение по предыдущему. В программе использованы следующие константы:

δdelta – отвечает за точность нахождения и m – максимальная размерность вводимой матрицы.

Введены  и описаны в модуле типы:

1.  matrix – двумерный массив mxm

2.   vector – одномерный массив из m компонент.

Процедуры:

1.  input(var dim:integer; A: matrix; var и,y:vector) – процедура получения матрицы,  точного решения и столбца правой части

2.  GetResult(dim:integer;A:matrix;b:vector;dt:myreal;var numit:integer):vector; - функция получения результата.

Численные эксперименты.

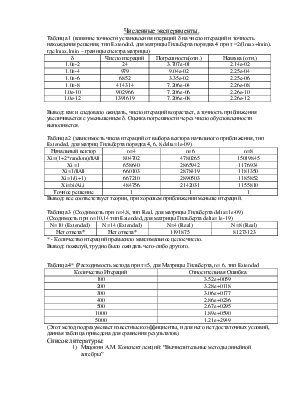
Таблица 1 (влияние точности установления итераций δ на число итераций и точность нахождения решения, тип Extended, для матрицы Гильберта порядка 4 при τ =2/(lmax+lmin), где lmax,lmin – границы спектра матрицы)

Вывод: как и следовало ожидать, число итераций возрастает, а точность приближения увеличивается с уменьшением δ. Оценка погрешности через число обусловленности выполняется.

Таблица 2 (зависимость числа итераций от выбора вектора начального приближения, тип Extended, для матриц Гильберта порядка 4, 6, 8,delta=1e-09)

Вывод: все соответствует теории, при хорошем приближении меньше итераций.

Таблица 3 (Cходимость при n=4,8, тип Real, для матрицы Гильберта delta=1e-09)

(Сходимость при n=10,14 тип Extended, для матрицы Гильберта delta=1e-19)

* - Количество итераций превысило максимальное целое число.

Вывод: пожалуй, трудно было ожидать чего-либо другого.

Таблица 4* (Расходимость метода при τ=5, для Матрицы Гильберта, n= 6, тип Extended

(Этот метод подразумевает известные коэффициенты, и для него нет достаточных условий, данная таблица приведена для сравнения результатов)

Список литературы:

1)  Мацокин А.М. Конспект лекций: “Вычислительные методы линейной алгебры”