














§ 8. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
8.1. Понятие случайной величины. Дискретные и непрерывные случайные величины.
Интерес к изучению случайных событий связан в первую очередь с тем, что именно к ним относятся результаты большинства наблюдений. Случайным является число космических частиц, регистрируемых счетчиком за одну секунду. Случайными являются содержание сахара или гормонов в крови, рост и вес обследуемых пациентов и т.д. Даже самый точный метод анализа вещества дает при повторениях некоторое расхождение в результатах (ошибка воспроизводимости), значит, и здесь каждый числовой результат есть случайное событие. Таким образом, каждое случайное событие характеризуется количественным параметром. Например, случайное событие будет дождь или нет характеризуется количественным параметром сколько выпадет осадков, приход автобуса на остановку характеризуется временем прихода и т.п. В медицине и биологии рассматривают объект наблюдения, например, больного. В процессе наблюдения выявляют пол больного, состояние заболевания, рост, вес, количественные данные лабораторных исследований и т.д. Отдельные параметры, например пол, являются качественными, другие, например рост, являются количественными. Мы рассмотрим только количественные параметры. Количественные параметры принимают определенные значения, но заранее неизвестно какие, т.е. случайные.
Рассмотренные примеры приводят нас к важному понятию случайной величины. Случайной величиной называется величина, принимающая в результате испытания числовое значение, которое нельзя предсказать, исходя из условий испытания.
Случайная величина обладает целым набором допустимых значений, но в результате каждого отдельного испытания принимает лишь какое-то одно из них. Очень важно отметить, что случайная величина может принимать различные значения даже при неизменном комплексе основных факторов. Причина изменения случайной величины от испытания к испытанию кроется в не учитываемых нами факторах, которые мы назвали случайными.
Случайные величины имеют свою классификацию. Случайная величина называется дискретной, если она принимает строго определенные значения и других значений между ними быть не может.
Каждое значение дискретной величины отделено от соседних некоторыми промежутками, как бы оторвано от них, поэтому такую величину иногда называют прерывной. В качестве примера дискретной случайной величины можно рассмотреть число зрителей в зрительном зале, число студентов на лекции, число зерен в колосе и т.д.
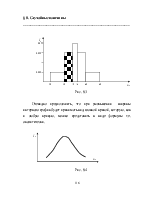
Если значения случайной величины могут сплошь заполнять некоторый промежуток, как, например, рост человека или его вес, то эти значения уже нельзя отделить друг от друга промежутками. Следовательно, случайная величина с таким набором допустимых значений уже не будет дискретной.
Такие случайные величины называют непрерывными. Случайная величина называется непрерывной, если она может принимать любое значение в заданном интервале.
Иногда, для удобства, непрерывную случайную величину представляют в виде дискретной. Например, размер стопы – непрерывная величина (12-40см), но при изготовлении обуви размер ее представляют в виде дискретной величины 22, 23, 24, 30
Как было отмечено выше случайная величина может выражаться как числом, так и качественным признаком. Например, самочувствие больного может быть отражено с помощью температуры, давления, содержания гормонов в крови и т.д., а может быть отражено с помощью таких показателей, как «удовлетворительное, неудовлетворительное, хорошее». Качественные признаки также являются случайными величинами, но так как их нельзя описать с помощью количественных параметров, они изучаются непараметрическими методами, которые мы не рассматриваем.
8.2. Генеральная и выборочная совокупности. Распределение случайной величины.
Применение методов математической статистики к обработке наблюдений оказывается возможным благодаря тому, что производство наблюдений полностью соответствует основной схеме статистических испытаний, называемой выборочным методом.
Выборочный метод в самой общей форме выглядит следующим образом. Имеется некоторая большая совокупность объектов, называемая генеральной совокупностью (Совокупность всех значений какого-то признака объектов называется генеральной совокупностью).
Из этой совокупности извлекаются n объектов, которые образуют выборку (выборка – часть генеральной совокупности, взятая для исследования); число n называется объемом выборки. Эти nобъектов подвергаются детальному исследованию, по результатам которого требуется описать всю генеральную совокупность или какие-нибудь ее свойства, характеристики.
Приведем простой пример применения выборочного метода
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.