Рабочая программа дисциплины «Теоретическая механика» (Структура и содержание курса. Содержание самостоятельной работы студентов, график ее выполнения), страница 8

Работа на практических занятиях и выполнение домашних заданий характеризует регулярность работы студента. РГЗ определяют степень усвоения студентом изучаемого курса и играют решающую роль в получении зачета.

РГЗ 1.  Пример

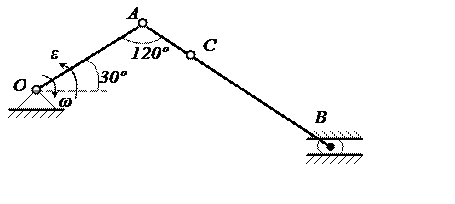Кривошип ОА вращается  вокруг оси О, имея угловую скорость ω = 2 с^-1. Угловое ускорение ε = 3 с^-2. Определить в указанном на чертеже положении скорости и ускорения точек А, В, С шатуна.

Дано: АВ = 40 см; АС = 10 см, ОА = 20 см.

Плоское движение состоит из двух простых движений: поступательного и вращательного. Поэтому при выполнении и защите этого задания студенты должны знать определение указанных видов движения, уравнения (закон) движения, способы нахождения скоростей и ускорений точек тел для каждого движения.

РГЗ 2.  Пример

На криволинейный стержень АВС действует момент  М = 2 кН·м, сила Р = 4 кН, распределенная нагрузка q = 1,5 кН/м,  α = 30º, ВD = DС. Найти, при каком способе закрепления реакции У_А имеет минимальное значение по модулю, и для этого способа закрепления найти остальные реакции.

При выполнении этого задания нужно уметь правильно изображать реакции связей и знать формы уравнений равновесия произвольной плоской системы сил.

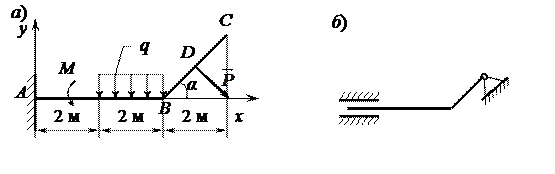При нахождении исследуемой реакции полезно помнить, что оси координат можно выбрать и по-другому, а точка, относительно которой составляются моменты сил, произвольна.

4.2  Технология и методическое обеспечение аттестации студентов

по курсу в третьем семестре

В соответствии с рабочим учебным планом в третьем семестре предусмотрена аттестация студентов по курсу в виде письменного экзамена с последующей беседой с преподавателем. Условием допуска студента к экзамену является выполнение и защита расчетно-графического задания и выполнение контрольной работы.

РГЗ 1. Пример.  Каток массы m₁ = 8 кг, радиуса R₁ = 20 см под действием момента М = 20Н·м катится без скольжения по горизонтальной поверхности и с помощью нити, перекинутой через неподвижный двухступенчатый шкив 2 массы m₂ = 2 кг, приводит в движение груз 3 массы m₃ = 10 кг, скользящий по шероховатой поверхности, наклоненной под углом α = 30º к горизонту.

Найти скорость груза, когда центр катка переместится на расстояние S = 2 м.

Коэффициент трения качения f_к = 0,1 см, коэффициент трения скольжения f = 0,1. Каток считать сплошным однородным цилиндром. Масса шкива, имеющего радиусы r₂ = 10 см, R₂ = 20 см, распределена по ободу большого радиуса. В начальный момент система находилась в покое.

При решении этого задания следует знать выражение кинетической энергии поступательного, вращательного и плоского движений тела, как вычисляется работа силы и момента силы, теорему об изменении кинетической энергии механической системы. Нужно также помнить, как вычисляются скорости точек тела при поступательном, вращательном и плоском движении.

Контрольная работа. Пример.  Шофер автомобиля, движущегося со скоростью 72 км/ч, за 30 м до препятствия нажал на тормоз, блокируя колеса. Коэффициент трения скольжения f = 0,5. Остановится ли автомобиль до препятствия? Какова должны была быть безопасная скорость в этом случае?

4.2.1  Теоретические вопросы, выносимые на экзамен

1)  Законы и задачи динамики.

2)  Дифференциальные уравнения движения материальной точки в декартовых координатах и естественных.

3)  Дифференциальные уравнения относительного движения материальной точки.

4)  Свободные прямолинейные колебания материальной точки.

5)  Механическая система. Центр масс. Внешние и внутренние силы. Свойства внутренних сил. Дифференциальные уравнения движения механической системы.

6)  Теорема о движении центра масс и ее следствия.

7)  Количество движения точки и механической системы. Выражение количества движения механической системы через скорость центра масс.

Теорема об изменении количества движения точки и системы в дифференциальной и интегральной форме. Следствия.

8)  Понятие о моментах инерции. Моменты инерции симметричных тел. Теорема Гюйгенса-Штеймера.

9)  Момент количества движения точки. Момент количества движения (кинетический момент) механической системы. Кинетический момент тела относительно оси вращения.