Мощность разбаланса и пульсации мгновенной мощности при симметричном напряжении

МОЩНОСТЬ РАЗБАЛАНСА И ПУЛЬСАЦИИ МГНОВЕННОЙ МОЩНОСТИ

ПРИ СИММЕТРИЧНОМ НАПРЯЖЕНИИ

Ю.А. Сиротин, к.т.н., доцент

Национальный технический университет

"Харьковский политехнический институт"

Исследование автором [1-3] разбаланса трехфазного энергетического  интерфейса «поставщик–потребитель» было вызвано необходимостью количественной оценки вклада в ухудшение качества электроэнергии отдельно потребителем и поставщиком. Проведенные для  синусоидального  установившегося  несимметричного режима исследования  потребовали введения математического аппарата, который ранее в электроэнергетике не использовался (введение вектора мощности разбаланса, разложения трехфазного вектора (3-D комплекса) тока на ортогональные компоненты, понятие базиса несимметричных компонент и т.д. [1-3]). Анализ ухудшения  качества потребления при несимметричной (точнее, при несбалансированной)  нагрузке был проведен   разложением полной мощности на квадратичные компоненты. При такой  нагрузке (как при симметричном, так и несимметричном  напряжении) уравнение мощности содержит мощность разбаланса и характеризует потери мощности от небаланса нагрузки. [1-3].

Другой интегрированной  характеристикой  ухудшения качества поставки  и потребления в несимметричном режиме являются пульсации мгновенной мощности [4-7]. Как известно, при симметричных синусоидальных величинах напряжений и токов (в отличие от однофазной цепи – даже при ненулевой реактивной мощности) в точке подключения линейной нагрузки к трёхфазной распределительной сети не только отсутствуют обменные процессы (осцилляции потока энергии), но даже не наблюдаются пульсации мгновенной мощности  (система уравновешена [5, 8], сбалансирована [7]). В трёхфазной системе уже в синусоидальном режиме пульсации мгновенной мощности (ММ)  наблюдаются только тогда, когда она работает в режиме, для которого она не проектировалась: при несимметричном напряжении или/и асимметричной линейной нагрузке. Пульсации ММ физически наблюдаемое явление и  их амплитуда имеет размерность мощности.  В однофазной цепи с синусоидальными процессами амплитуда пульсаций (осцилляций) равна реактивной мощности, однако для трехфазной цепи это не так.  В [6] показано, что при синусоидальном симметричном напряжении и линейной асимметричной нагрузке типа треугольник амплитуда колебательной компоненты никак не связана с реактивной мощностью и равна мощности разбаланса. В  [4] предложено  амплитуду пульсаций (вместо мощности разбаланса) включить в уравнение мощности (однако, как показано ниже, для четырехпроводной системы даже при симметричном напряжении это неверно).

Задача заключается в том, чтобы выяснить, как пульсации ММ связаны с мощностью разбаланса для четырехпроводной системы. В [1-3] показано, что в такой системе  небаланс нагрузки более полно может быть описан не мощностью разбаланса, а вектором мощности разбаланса (который вычисляется как векторное произведение 3D-комплексов тока и напряжения). Такое описание справедливо и для трёх-, и для четырёхпроводной системы, при симметричном и асимметричном напряжениях. Норма вектора мощности разбаланса равна мощности разбаланса и удовлетворяет уравнению мощности для несбалансированной (асимметричной) нагрузки.

В настоящей работе получены симметричные составляющие вектора мощности. Показано, что при симметричном напряжении как в четырех-, так и в трехпроводной системе только  нулевая последовательность введённого вектора мощности определяет амплитуду пульсаций ММ. При этом пульсации ММ никак не связаны с реактивной мощностью, которая определяет только фазовый сдвиг между током прямой последовательности и симметричным напряжением.

Таким образом, используя вектор мощности разбаланса, можно  вычислять вклад от небаланса нагрузки не только в дополнительные потери мощности, но и в пульсации ММ.  Как будет показано в дальнейших исследованиях это утверждение справедливо и при несимметричном напряжении.

Трёхфазный интерфейс "поставщик–потребитель". В трёхпроводном сечении  трёхфазной системы в синусоидальном режиме мгновенные значения трёхфазного напряжения и тока

,                                           (1)

(2)

однозначно определены трёхмерными комплексными векторами (3D-комплексами) напряжений  и токов  – векторами комплексных действующих величин

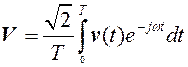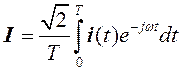,        ,                       (3) где  – знак транспонирования,  – период ().

Мгновенная мощность (скорость передачи энергии) в сечении , к которому приложены напряжения (1) и протекают токи (2), может быть выражена через 3D-комплексы напряжения и тока (3)