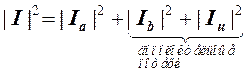Мощность разбаланса и пульсации мгновенной мощности при симметричном напряжении, страница 3

,       

.                      (25)

Ток небаланса, увеличивая дополнительные потери, вызывает несимметричное падение напряжения, ухудшает качество электроэнергии. Коэффициент мощности (отношение активной мощности к полной мощности) определяется отношением действующего значения активного тока к действующему значению полного тока

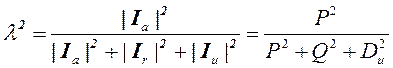                            (26)

Базис симметричных компонент и КМ пульсаций. В пространстве 3D- комплексов (трёхмерных векторов с комплексными коэффициентами) орты положительной, отрицательной и нулевой последовательностей определены как [3]

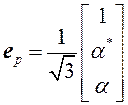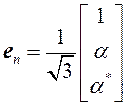,       ,          .                              (27)

Здесь (, , ).

3D-комплексы (27) попарно ортогональны

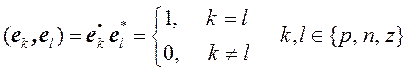                                       (28)

и определяют ортонормированный базис. Любой 3D-комплекс (трёхмерный вектор с комплексными координатами) может быть единственным способом записан как сумма трёх попарно ортогональных векторов

.                                    (29)

Комплексный коэффициент

                                                (30)

ортогонального разложения (29) является ортогональной проекцией вектора  на вектор .

В базисе (27) векторы напряжений и токов (3) можно записать как

,                                      (31)

 .                                      (32)

Так как , то в силу линейности скалярного произведения и ортогональности базиса (27) для КМ пульсаций имеем (8)

 .                      (33)

Так как ,    и , то для стандартной КМ (5) справедливо

 ,                        (34)

Симметричные компоненты вектора мощности разбаланса. Векторные произведений ортов симметричного базиса (27) можно представить  таблицей:

Используя вышеприведенную  таблицу векторных произведений для вектора мощности разбаланса (18)

,                                     (35)

получим выражения для его симметричных координат

,           (36a)

,         (36б)

.             (36в)

Симметричное напряжение и разложение тока.

Если в трёхпроводном сечении  напряжение симметрично прямой последовательности  (в симметричных координатах ), то для вектора тока и вектора мощности разбаланса (15) имеем

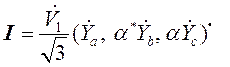,           (38) 

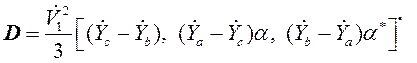,        (39)

где  – эквивалентные проводимости (12).

Симметричные координаты (32) вектора тока (38)

,       ,                        (40)

вычисляются через проводимости прямой, обратной и нулевой последовательностей

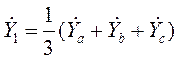,            ,                                    (41а)

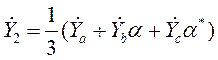,        ,                                 (41б)

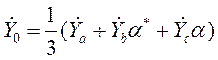.        ,                               (41в)

что для вектора тока даёт

.          (42)

Вектор мощности разбаланса и пульсации ММ.

При симметричном напряжении () для вектора мощности разбаланса (36) в симметричных координатах

                   (43)

компонента обратной последовательности равна нулю , его компонента  задана током нулевой последовательности, а компонента – током обратной последовательности.

Вектор тока небаланса равен сумме векторов тока обратной и нулевой последовательности (40)   и определяет мощность разбаланса

 .                       (44)

Так как комплексно-сопряжённый вектор напряжения прямой последовательности является вектором обратной последовательности (), то он ортогонален векторам тока прямой и нулевой последовательностей  и  ( или  и ) . Поэтому КМ пульсаций (8) обусловлена только током обратной последовательности, и

.            (45)

Таким образом, если норма (действующая величина) вектора мощности разбаланса равна мощности разбаланса и удовлетворяет уравнению мощности (19), то нулевая составляющая  этого вектора определяет амплитуду пульсаций ММ

                 (46)

и не может дополнять квадрат геометрической мощности (17) до квадрата полной мощности (16), как утверждается в [4].

Из (45) следует, что КМ пульсаций

             (47)

полностью определена проводимостью обратной последовательности, что для ММ даёт

.                     (48)

Из (48) следует, что осцилляции ПЭ будут при условии . Если нагрузка чисто активная , но асимметричная , то из (41б)–(41в) следует, что , и . Тогда при чисто активной нагрузке для ММ имеем

 .                           (49)

В трёхпроводной системе , и вектор мощности разбаланса содержит только компоненту нулевой последовательности (ток небаланса равен току обратной последовательности)

,   , что соответствует результату [6]:

.              (50)