![]() . (4)
. (4)
Первое слагаемое в (4) является стандартной комплексной мощностью (КМ)
![]() (5)
(5)
с квадратурными компонентами (активной и реактивной мощностью)
![]() ,
, ![]() ,
, ![]() . (6)
. (6)
и амплитудно-фазовыми составляющими (модулем и фазой)
![]() ,
, ![]() ; (7)
; (7)
второе слагаемое является комплексной мощностью (КМ) пульсаций [4] (alternatecomplexpower [7])
![]() .
. ![]() . (8)
. (8)
Здесь и дальше ![]() означает определение левой части выражения
через правую часть.
означает определение левой части выражения
через правую часть.
Если стандартная КМ равна скалярному произведению векторов тока и напряжения (3),
то КМ пульсаций (8) равна скалярному произведению 3D-комплекса тока (3) и комплексно-сопряжённого
вектора напряжений ![]()
![]() , (9)
, (9)
![]() . (10)
. (10)
Мгновенная мощность (4) может быть записана как
![]() . (11)
. (11)
Для трёхпроводного сечения![]() определим эквивалентные
проводимости фаз
определим эквивалентные
проводимости фаз
![]()
![]() (12)
(12)
где ![]() – разность фаз между током и напряжением
в k-фазе.
– разность фаз между током и напряжением
в k-фазе.
Если в трёхпроводном сечении подключена нагрузка типа звезды с заземленной нейтралью, то введённые проводимости (12) равны проводимостям фаз нагрузки.
Если эквивалентные проводимости (12) во всех фазах одинаковы
![]()
![]() , (13)
, (13)
то
![]() , (14)
, (14)
и пара векторов напряжений и токов (3) комплексно коллинеарны (![]() ), а трёхфазные синусоидальные
величины напряжений (1) и токов (2) сбалансированы (уравновешены) [2,3].
), а трёхфазные синусоидальные
величины напряжений (1) и токов (2) сбалансированы (уравновешены) [2,3].
Если в этом сечении подключена нагрузка типа звезды с заземлённой
нейтралью, то условие (14) означает, что нагрузка симметрична. Однако для
нагрузки типа треугольник с межфазными проводимостями ![]() это не так. Если в сечении
это не так. Если в сечении ![]() подключена
подключена ![]() нагрузка,
то фазовые токи
нагрузка,
то фазовые токи ![]() и узловые напряжения
и узловые напряжения ![]() в трёхпроводном сечении связаны между
собой матричным уравнением
в трёхпроводном сечении связаны между
собой матричным уравнением ![]() с матрицей узловых проводимостей
с матрицей узловых проводимостей ![]() нагрузки
нагрузки
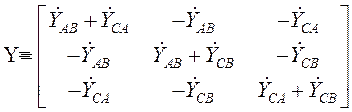 .
.
Типичным примером [9, 10]
такой несимметричной (но сбалансированной) нагрузки является схема симметризации
Штейница, когда однофазная активная нагрузка ![]() дополняется до
дополняется до ![]() нагрузки реактивными элементами
нагрузки реактивными элементами ![]() ,
, ![]() . Согласно (14), такая
. Согласно (14), такая ![]() нагрузка сбалансирована с симметричным
напряжением (можно проверить, что
нагрузка сбалансирована с симметричным
напряжением (можно проверить, что![]() ). Таким образом, если выполнено (14), и в этом сечении
подключена нагрузка, то будем говорить, что нагрузка сбалансирована.
). Таким образом, если выполнено (14), и в этом сечении
подключена нагрузка, то будем говорить, что нагрузка сбалансирована.
В общем случае для любых векторов напряжений и токов (3) (при несимметричном напряжении и несбалансированной нагрузке) справедливо тождество [1]
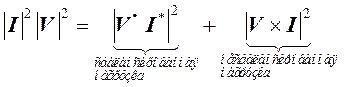 . (15)
. (15)
Произведение
действующих величин (норм) трёхфазного вектора тока ![]() и вектора напряжения
и вектора напряжения ![]() определяет полную мощность по Buchholz' [11]
определяет полную мощность по Buchholz' [11]
![]() . (16)
. (16)
Модуль
комплексной мощности ![]() определяет
геометрическую мощность трёхфазной нагрузки [3]
определяет
геометрическую мощность трёхфазной нагрузки [3]
![]() . (17)
. (17)
Векторное произведение комплексных векторов напряжений и токов (3)
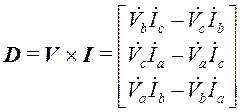 (18)
(18)
вычисляется подобно векторному произведению обычных трёхмерных векторов (с вещественными координатами).
Так как
компоненты вектора (18) ![]() имеют размерность мощности
(вольтамперы), и
имеют размерность мощности
(вольтамперы), и ![]() только если нагрузка сбалансирована (симметрична для
нагрузки типа звезда), то его можно назвать вектором мощности небаланса
(несимметрии) нагрузки. Вводя обозначение для нормы вектора мощности
только если нагрузка сбалансирована (симметрична для
нагрузки типа звезда), то его можно назвать вектором мощности небаланса
(несимметрии) нагрузки. Вводя обозначение для нормы вектора мощности ![]() из (15), имеем уравнение мощности
для несимметричной нагрузки
из (15), имеем уравнение мощности
для несимметричной нагрузки
![]() . (19)
. (19)
Уравнению мощности (19) соответствует разложение вектора тока [2]
![]() .
(20)
.
(20)
на две ортогональные компоненты: ток
баланса ![]() и ток небаланса
и ток небаланса![]() .
.
Ток
баланса ![]() является
ортогональной проекцией вектора тока на вектор напряжения (относительно скалярного
произведения (9)), а ток небаланса – его ортогональное дополнение. Ток баланса –
это ток с минимальной действующей величиной, который при заданном напряжении
передаёт в нагрузку ту же активную и реактивную мощность. Можно показать [2],
что
является
ортогональной проекцией вектора тока на вектор напряжения (относительно скалярного
произведения (9)), а ток небаланса – его ортогональное дополнение. Ток баланса –
это ток с минимальной действующей величиной, который при заданном напряжении
передаёт в нагрузку ту же активную и реактивную мощность. Можно показать [2],
что
![]() ,
, ![]() . (21)
. (21)
Теорема Пифагора для векторов токов (20) и уравнение мощности (19) – равносильные утверждения
![]()
![]()
![]() . (22)
. (22)
Вектор тока баланса ![]() (
(![]() ) комплексно коллинеарен вектору напряжения (
) комплексно коллинеарен вектору напряжения (![]() ) и может быть разложен на две компоненты:
) и может быть разложен на две компоненты:
 ,
, 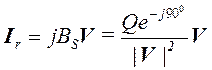 , (23)
, (23)
что даёт разложение тока [2]
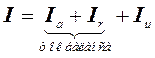 (24)
(24)
При несбалансированной нагрузке дополнительные потери определяются не только реактивным током (мощностью), но и током (мощностью) небаланса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.