Линейные электрические цепи постоянного тока. Определение токов во всех ветвях цепи методом контурных токов

Задание 1

Задача 1.1 Линейные электрические цепи постоянного тока

Дана электрическая схема (рис. 1).

1. Составить систему уравнений для определения токов по закону Кирхгофа;

2. записать для цепи законы Кирхгофа в матричной форме;

3. Определить токи во всех ветвях цепи методом контурных токов (МКТ) и записать в матричной форме;

4. Проверить правильность решения, применив метод узлового напряжения, предварительно упростив схему, заменив треугольник сопротивлений r₄, r₅, r₆ эквивалентной звездой. Начертить расчётную схему с эквивалентной звездой и показать на ней токи;

5. Определить сопротивление резистора r₆ методом эквивалентного генератора;

6. Определить показания вольтметра и составить баланс мощностей для заданной схемы;

7. Построить в масштабе потенциальную диаграмму для любого замкнутого контура цепи, включая обе ЭДС.

r6

Дано:

r5

r4

Е₁ = 40 В              r₁ = 3 Ом

r1

Е₂ = 25 В              r₂ = 3 Ом

E2, r02

E3, r03

Е₃ = 8 В                r₃ = 2 Ом

r₀₁ = 0 Ом              r₄ = 4 Ом

r₀₂ = 0,2 Ом          r₅ = 3 Ом

Рисунок 1.

r2

r3

E1, r01

r₀₃ = 0,2 Ом                    r₆ = 2 Ом
I. Определение токов по закону Кирхгофа.

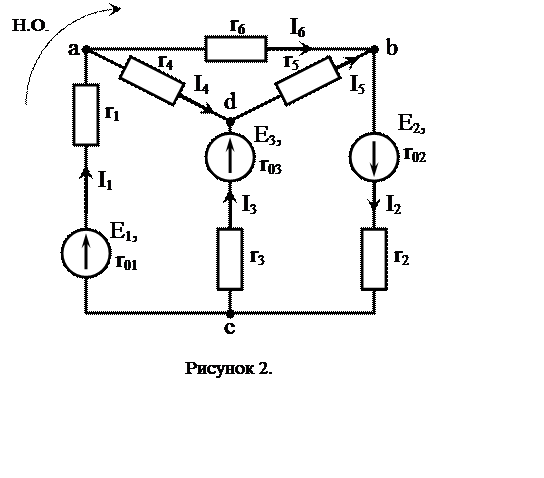
1. Произвольно задаёмся положительными направлениями токов в ветвях и направлением обхода (рисунок 2, в данном случае по часовой стрелке). Число необходимых уравнений для электрической цепи равно числу ветвей (число ветвей b = 6).

2. Составляем уравнение по первому закону Кирхгофа, которые на единицу меньше числа узлов (т.е. у – 1 = 4 – 1 = 3). Запишем уравнение для узлов а, b, c. Токи, направленные к узлу возьмем со знаком «+», а от узла со знаком «–».

Узел ”а”                                    ;

Узел ”b”                                   ;                                           (1.1)

Узел ”с”                                    ;

3. Недостающее число уравнений (т.е. b – (у – 1) = 6 – 3 = 3) составляются по второму закону Кирхгофа. Для нашего примера необходимо составить еще три уравнения для независимых контуров электрической цепи. При составлении уравнений падение напряжения и ЭДС записываются с положительными знаками, если направление тока в сопротивлении контура и ЭДС совпадают с направлением обхода контура и наоборот.

Контур «adca»               ;

Контур «abda»

(1.2)

               ;

Контур «bcdb»               ;

Решая полученную систему шести уравнений, можно определять токи в ветвях. Если какой-либо ток в результате расчета получается отрицательным, то это означает, что его действительное направление противоположно произвольно выбранному направлению.

II. Матричная форма записи уравнений Кирхгофа.

Матричная форма записи уравнения Кирхгофа имеет вид:

                                                 (2.1)

где: [A] и [B] – квадратные матрицы коэффициентов при токах и напряжениях;

[I] и [E] – матрицы-столбцы неизвестных токов и заданных ЭДС.

Элементы матриц [A] являются коэффициенты при токах в левой части уравнений, составленных по законам Кирхгофа.

Первые строки (у – 1) матрицы [A] содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1,    –1, 0 в зависимости от того, с каким знаком входит ток в уравнение. Элементы следующих (b – y + 1) строк матрицы [A] равны значениям сопротивлений при соответствующих токах, в уравнениях, составленных по второму закону Кирхгофа. Для данной электрической схемы квадратная матрица [A] типа b*b будет иметь вид:

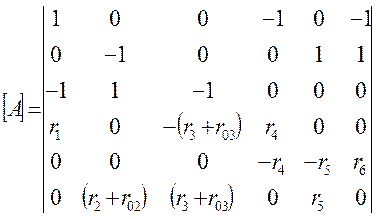                                    (2.2)

Элементы матрицы [B] равны коэффициентам при ЭДС в правой части уравнений. Первые (у-1) строки матрицы имеют нулевые элементы, т.к. ЭДС в правой части уравнений, записанных по первому закону Кирхгофа, отсутствуют. Остальные (b-y+1) содержат элементы +1, –1, 0 в зависимости от того, с каким знаком входит ЭДС в уравнение (0, если ЭДС в уравнение не входит).