Для общности записи в уравнения (1.2) в ветвях 4, 5, 6 включены ЭДС, равные нулю (Е4 = Е5 = Е6 = 0).
![]()
![]() ;
;
![]() ;
(2.3)
;
(2.3)
![]() ;
;
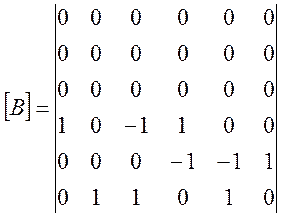 (2.4)
(2.4)
 ;
; 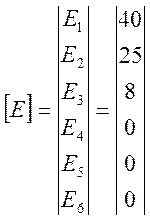 (2.5)
(2.5)
Рассмотренный метод применения законов Кирхгофа является довольно громоздким из-за большого количества уравнений, поэтому расчет целесообразно вести другими методами, позволяющими уменьшить количество уравнений.
III. Метод контурных токов.
Метод заключается в том, что вместо действительных токов в ветвях на основании второго закона Кирхгофа определяют контурные токи в независимых контурах.
Контурным будет такой расчетный (условный) ток, который замыкается только по своему контуру.
Действительный ток в любой ветви, принадлежащей только одному контуру, численно равен контурному току, а в ветви, принадлежащей нескольким контурам, равен алгебраической сумме контурных токов. Число уравнений, составляемых по второму закону Кирхгофа, равно числу независимых контуров (N = b – у + 1).
Последовательность расчета цепи следующая:
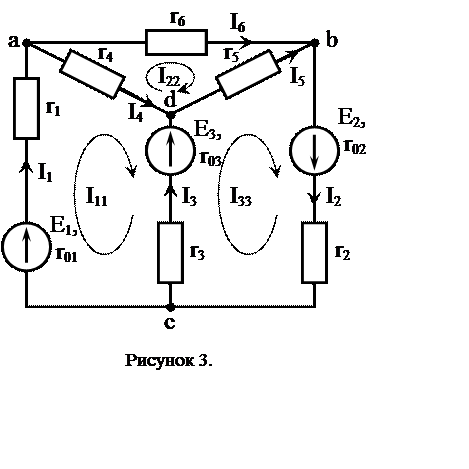 |
2. Cоставляем для каждого контура уравнение по второму закону Кирхгофа. В результате получаем систему трёх уравнений относительно контурных токов:
![]()
![]() ;
;
![]() ; (3.1)
; (3.1)
![]() .
.
Подставим значение сопротивлений и ЭДС.
![]()
![]() ;
;
![]() ;
;
![]() .
.
Дальнейший расчёт ведём методом определителей.
3. Находим главный определитель (детерминант) системы:
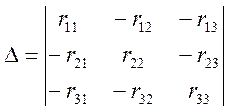 (3.2)
(3.2)
где: r11, r22, r33 – собственные сопротивления контуров;
r12 = r21 = r4, r13 = r31 =r3 + r03, r23 = r32 = r5 – сопротивление смежных контуров.
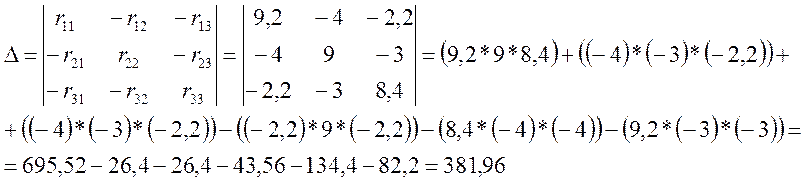
Каждый частный определитель Δk получают путём замены в главном определителе системы Δ k-того столбца сопротивлений столбцов контурных ЭДС, записанных в левой части системы уравнений (3.1).
При нахождении тока в первом контуре (k = 1), частный определитель имеет вид:
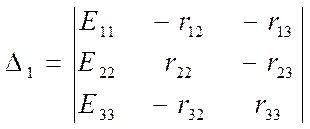 , где Е11; Е22;
Е33 – контурные ЭДС.
, где Е11; Е22;
Е33 – контурные ЭДС.
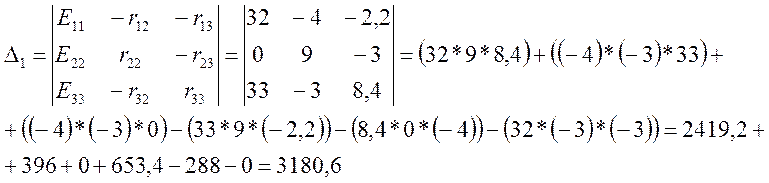
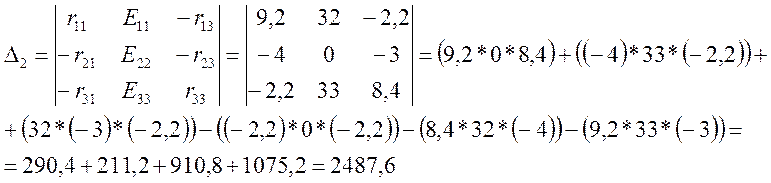
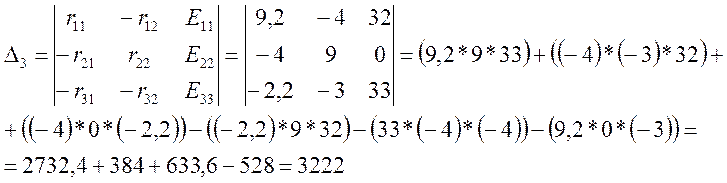
4. Контурные токи системы будут:
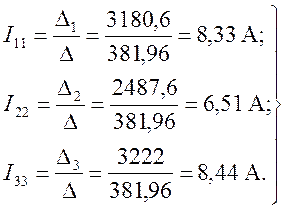 (3.3)
(3.3)
Находим значения действительных токов в ветвях схемы и их истинное направление:
![]() А;
А;
![]() А;
А;
![]() А;
А;
![]() А;
А;
![]() А;
А;
![]() А;
А;
Систему уравнений (3.1) можно решить с помощью матриц.
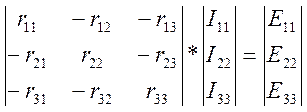 (3.4)
(3.4)
или в виде одного матричного уравнения
![]() (3.5)
(3.5)
где: ![]() - матрица столбцов неизвестных токов;
- матрица столбцов неизвестных токов;
![]() -
матрица, обратная матрице коэффициентов;
-
матрица, обратная матрице коэффициентов;
![]() -
матрица столбец свободных членов уравнения (контурных ЭДС).
-
матрица столбец свободных членов уравнения (контурных ЭДС).
Решение уравнений производится в следующей последовательности:
1. Составляется определитель Δ из элементов матрицы;
2. Составляем обратную матрицу для него:
а) каждый элемент матрицы коэффициентов заменяют алгебраическим дополнениями с теми же нижними коэффициентами, которые имеют заменяемые ими элементы;
б) транспортируют полученную матрицу алгебраических дополнений, для чего строки и столбцы её взаимно меняют местами;
в) делят полученную транспортированную матрицу на определитель Δ.
В результате этих действий обратную матрицу можно записать в виде выражения:
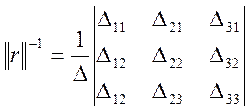 (3.6)
(3.6)
Коэффициенты Δnk представляет собой алгебраическое дополнение, связанные с минором Мnk, определителя уравнением.
![]() (3.7)
(3.7)
Минор получают из определителя вычёркиванием в нём строки n и столбца k. Для первого контура тока I11 алгебраические дополнения равны:
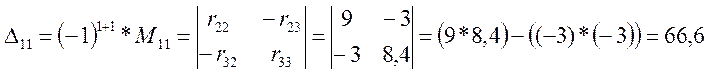
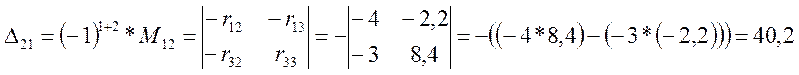
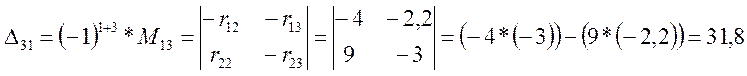
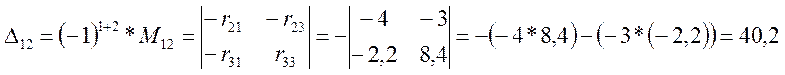
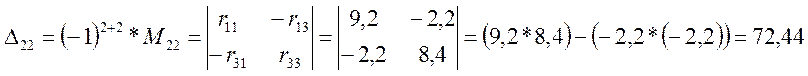
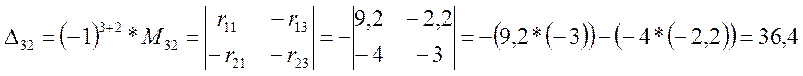
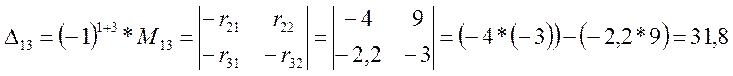
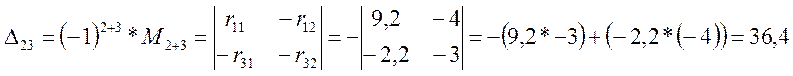
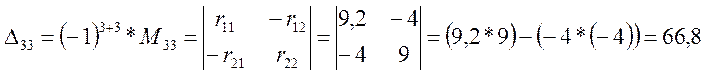
Уравнение (3.7) переписываем в развёрнутой форме.
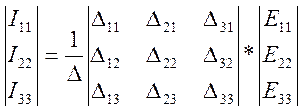 (3.8)
(3.8)
Перемножим две матрицы правой части уравнения (3.8).
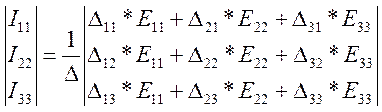 (3.9)
(3.9)
Матрицы равны, если равны их элементы, поэтому
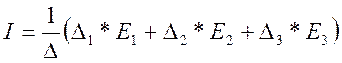 (3.10)
(3.10)
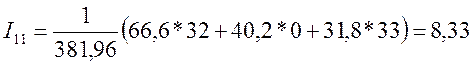 А;
А;
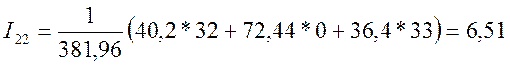 А;
А;
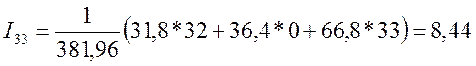 А.
А.
IV. Метод двух узлов.
Применим данный метод для определения токов в схеме рисунка 1. Для этого, заменив в схеме рисунка 1. треугольник сопротивлений r4, r5, r6, эквивалентной звездой. Получим эквивалентную схему (рисунок 4).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.