Линейные электрические цепи постоянного тока. Определение токов во всех ветвях цепи методом контурных токов, страница 3

Сопротивление лучей эквивалентной звезды определяется из выражения:

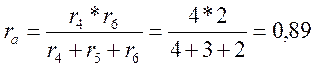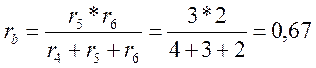 Ом;

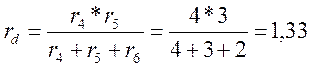 Ом;

 Ом.

Задаёмся произвольным напряжением узлового напряжения U_an и находим его величину по формуле:

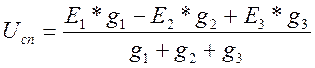 , В;

где: g₁, g₂, g₃ – проводимость ветвей; См.

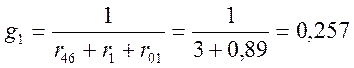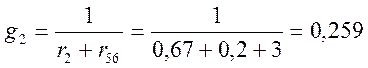 См;

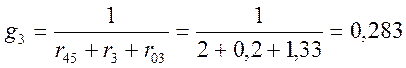 См;

 См;

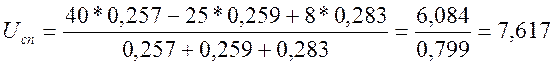 В.

Выберем условное положительное направление токов в ветвях и, в соответствии с обобщённым законом Ома для активной ветви, будем иметь:

 А;

 А;

 А.

V. Метод эквивалентного генератора.

Данный метод позволяет определить ток в одной рассматриваемой ветви активного двухполюсника. Поэтому многоэлементный активный двухполюсник, к которому подключена рассматриваемая ветвь, может быть заменена эквивалентным источником напряжения с параметрами E_экв и r_экв. Режим работы рассматриваемой ветви, присоединённой к активному двухполюснику при этом, не меняется.

Ток в рассматриваемой ветви определяется по формуле:

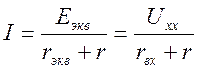                                                                            (5.1)

где: Е_экв – ЭДС эквивалентного генератора, равная воздействию источников питания активного двухполюсника на рассматриваемую ветвь. Это воздействие источников питания равно напряжению холостого хода – U_хх на клеймах рассматриваемой ветви.

r_экв – сопротивление эквивалентного генератора, равное входному сопротивлению r_вх пассивного двухполюсника.

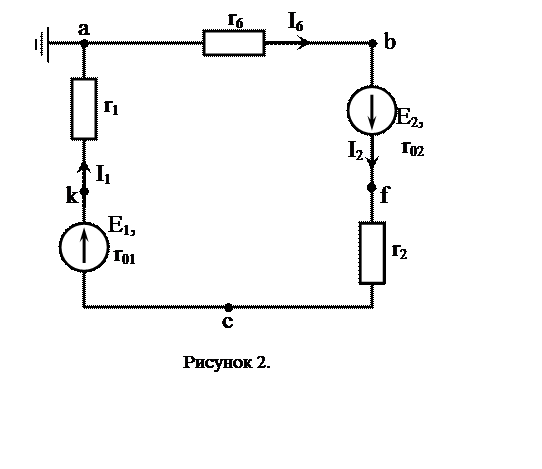
Применим метод эквивалентного генератора для схемы рисунка 1., для определения тока I₆.

С этой целью размыкаем ветвь с сопротивлением r₆ и находим напряжение холостого хода на зажимах разомкнутой ветви.

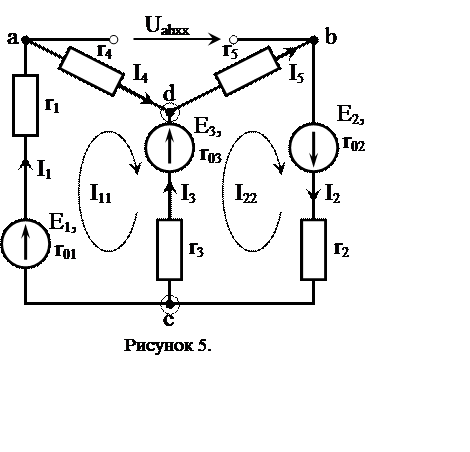Определим напряжение Uab, для этого запишем уравнения по 2-му закону Кирхгофа для контурных токов.

                       

                       

Решим систему уравнений с помощью определителя

   

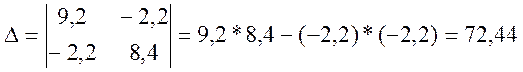
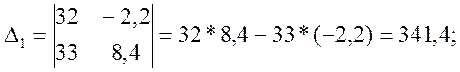
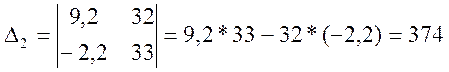
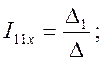
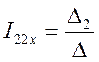
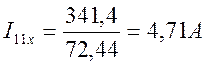
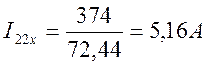
Составим уравнение по 2-му закону Кирхгофа для контура «adbUaba»

Для определения входного сопротивления схемы по отношению разомкнутых зажимов необходимо двухполюсник сделать пассивным, для чего закорачиваются источники питания.

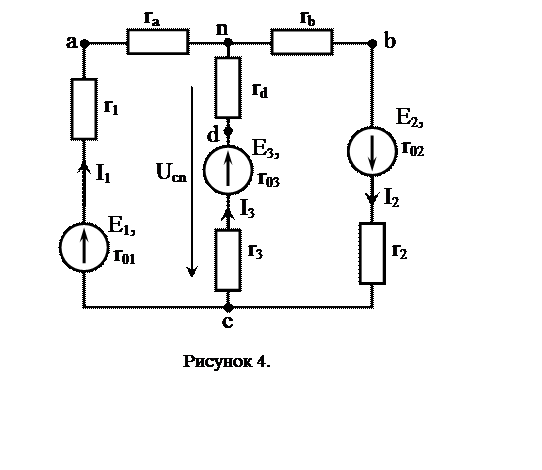
Заменим треугольник сопротивлений r₁; r₄; r₃ + r₀₃ эквивалентной звездой сопротивлений r_a; r_c; r_d (рисунок 6). Сопротивление лучей эквивалентной звезды определяется из выражения:

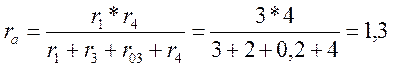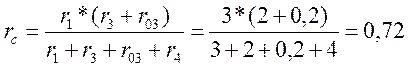 Ом;

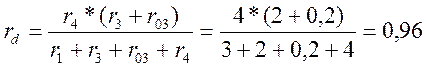 Ом;

Ом.

Входное сопротивление относительно зажимов «ab» равно

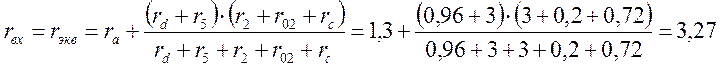 Ом;

Ток в рассматриваемой ветви с сопротивлением r₆ будет:

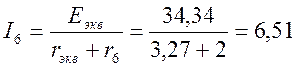А;

Полученное значение такое же, что и при расчете по методу контурных токов и методу двух.

VI. Энергетический баланс в электрических цепях и определение показания вольтметра.

Состояние энергетического баланса позволяет проверить правильность выполненных расчётов. В общем случае энергетический баланс определяется по выражению:

                                                            (6.1)

где: U_ad – напряжение между узлами a и d, к которым подтекает и утекает ток источника.

В данной схеме (рис. 1) источники тока отсутствуют, и уравнение баланса мощности будет иметь вид:

     (6.2)

В этом уравнении знак мощности будет положителен при совпадении направление ЭДС и тока, проходящего через источник, и отрицателен при взаимно противоположных направлениях ЭДС и тока.

После подстановки численных значений электрических величин,  имеем уравнение:

.

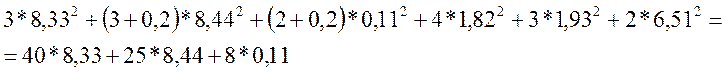
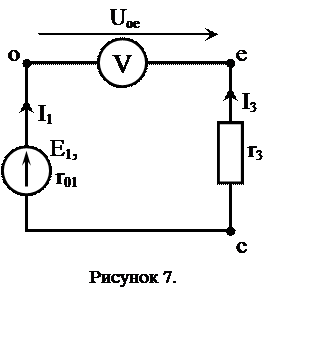
Определяем показания вольтметра. Для этого зарисуем схему контура «oeco», содержащего вольтметр (рисунок 7).

Согласно II-му закону Кирхгофа:

 В.

VII. Построение потенциальных диаграмм.

Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи по замкнутому контуру, построенный в прямоугольной системе координат, по которой по оси абсцисс откладывается в определённом масштабе сопротивления участков цепи, а по оси ординат – потенциалы соответствующих точек.

Строим потенциальную диаграмму для внешнего контура цепи изображенной на рисунке 1. Направление тока в ветвях указывается в соответствии с их расчётом      (рисунок 8).

Принимаем потенциал V_а = 0. Следует помнить, что в сопротивлении ток течёт от более высокого потенциала к более низкому, а стрелка внизу источника ЭДС указывает направление возрастания потенциала.

;

 В;

 В;

 В;

 В;

 В.

После полного обхода контура потенциал точки «а» остался равным  нулю, значит, потенциалы остальных точек найдены правильно.

Потенциальная диаграмма приведена на рисунке 9. Сопротивления откладываем в том порядке, как они встречаются при обходе контура.

 Ом.