Организация ЭВМ и систем: Курс лекций (Позиционные системы счисления. Процессоры семейства IA-32. Лазерные принтеры), страница 49

Первая исторически появившаяся оптимизация состоит в том, что страницы, предназначенные только для чтения, могут дублироваться. Это не понижает уровня согласованности. Но эта оптимизация ничего не даёт, если один процесс записывает одно слово вверху некоторой страницы, а другой процесс в то же самое время пытается записать другое слово внизу той же самой страницы. В таком случае страница передаётся туда и обратно. Данная ситуация называется ложным совместным использованием.

Проблему ложного совместного использования можно решить по-разному. Например, понизив согласованность от согласованности по последовательности до свободной согласованности. Страница может присутствовать в нескольких узлах одновременно, но при захвате критической области каким-либо процессом для записи все экземпляры, кроме захваченного объявляются недействительными.

Кроме DSM существует множество других систем, объединяющих память на логическом уровне. Различия в системах, помимо прочего, происходят от различных масштабов объединения, на которые рассчитана система: одни системы работают в пределах одной организации, другие рассчитаны на миллионы параллельных процессов, содержащие миллиарды объектов. Во втором случае дополнительные проблемы вносятся тем, что на каждой рабочей станции используются свои технологии дублирования, защиты и так далее.

Раздел 3 Вторичная память

16. Понятие о кодах с исправлением ошибок

[5]

Повышение надёжности хранения и передачи данных основывается на внесении избыточности.

Расстояние Хэмминга между двумя двоичными словами  и  равен количеству различающихся в них бит.

Например, интервал Хэмминга между словами 00010001 и 10010000 равен 2.

Нетрудно доказать, что интервал Хэмминга даёт метрику на множестве слов.

Если интервал Хемминга двух слов равен , то необходимо и достаточно  битовых ошибок, чтобы превратить одно слово в другое.

К слову, состоящему из  бит данных, добавляется  контрольных бит, которые однозначно определяются битами данных. В результате получается так называемое кодированное слово. Кодированное слово имеет длину , но из  комбинаций нулей и единиц допустимыми являются только .

Если в памяти обнаружено недопустимое кодированное слово, становится известно, что произошла ошибка. При определённых обстоятельствах её можно даже исправить.

Пусть  — множество всех допустимых слов для данного кода. Тогда интервалом Хэмминга кода называется величина .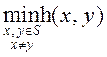

Именно интервал Хэмминга кода определяет возможности обнаружения и исправления ошибок. Действительно, чтобы обнаружить любые  ошибок в битах, необходим код с интервалом Хэмминга не менее .

Простейшим примером кода с обнаружением ошибок является код с битом чётности. Интервал Хэмминга этого кода равен 2. Он позволяет обнаружить одиночную ошибку в любом бите кодированного слова. Но он не позволяет исправить её.

Если интервал Хэмминга кода не менее , то можно исправить любые  ошибок в битах.

Теорема. Пусть  — множество допустимых слов кода с интервалом Хэмминга не менее .

Пусть далее, ;  — такое слово, что . (Поскольку интервал кода равен , .) Пусть  — такое допустимое слово, что .

Тогда .

Доказательство.

, поэтому . Поскольку интервал Хэмминга кода не менее , то отсюда следует .

Теорема доказана.

Главная проблема теперь — построение кода с заданным интервалом Хэмминга и минимальным количеством контрольных бит.

Прежде, чем рассматривать общий принцип, проиллюстрируем его на частном примере. Пусть требуется построить код для  с интервалом 3, то есть код, позволяющий не только обнаруживать, но и исправлять одиночные ошибки.

По одному биту четырёхбитного слова записывается в сектора, полученные пересечением кругов , ,  и , как указано на рисунке 16.1а.

Рис. 16.1. Код для четырёхбитных слов с интервалом 3 а — расположение битов данных б — биты данных и контрольные биты в — ошибка в первом бите данных

Добавляется три контрольных бита по одному в каждый из трёх кругов (рис. 16.1б). Контрольный бит показывает чётность бит, попадающих в его круг. При такой кодировке в каждом круге должно находиться чётное количество единичных бит.