





































![]() существовал
единственный обобщенный многочлен наилучшего приближения, необходимо и
достаточно, чтобы функции
существовал
единственный обобщенный многочлен наилучшего приближения, необходимо и
достаточно, чтобы функции ![]() образовывали систему
Чебышева, т.е. любой обобщенный многочлен по этой системе функций имел на
отрезке
образовывали систему
Чебышева, т.е. любой обобщенный многочлен по этой системе функций имел на
отрезке ![]() не более n различных нулей.
не более n различных нулей.
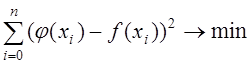 , (1)
, (1)
где ![]() –
точки, в которых задана функция
–
точки, в которых задана функция ![]() , причем
, причем ![]() .
.
В тех случаях, когда
известно, что значения ![]() имеют неодинаковую точность,
можно вводить веса
имеют неодинаковую точность,
можно вводить веса 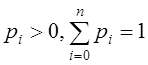 и минимизировать сумму
и минимизировать сумму
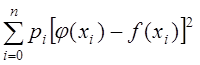 .
(2)
.
(2)
2. Линейная аппроксимация
Если в качестве
аппроксимирующих функций ![]() из линейного класса функций рассмотреть функции вида
из линейного класса функций рассмотреть функции вида ![]() и ограничиться случаем
и ограничиться случаем ![]() , тогда решение задачи
(1) означает, что неизвестную функцию
, тогда решение задачи
(1) означает, что неизвестную функцию ![]() аппроксимирует линейная функция вида
аппроксимирует линейная функция вида
![]() .
(3)
.
(3)
Такая аппроксимация возможна, когда
заданные точки ![]() располагаются вблизи некоторой
прямой линии. Проверить это можно либо визуально, нанеся такие точки на
плоскость либо аналитически рассчитав все отношения
располагаются вблизи некоторой
прямой линии. Проверить это можно либо визуально, нанеся такие точки на
плоскость либо аналитически рассчитав все отношения
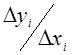 ,
(4)
,
(4)
где ![]() . Если
данные отношения будут примерно одинаковыми, линейная аппроксимация (3)
возможна. Коэффициенты
. Если
данные отношения будут примерно одинаковыми, линейная аппроксимация (3)
возможна. Коэффициенты ![]() и
и ![]() при этом задаются формулами
при этом задаются формулами
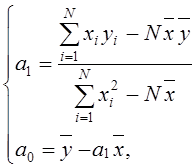 (5)
(5) 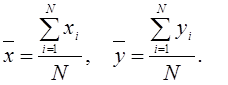
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1,0 |
2,1 |
3,0 |
3,9 |
4,9 |
6,0 |
|
|
1,5 |
3,1 |
4,6 |
6,0 |
7,5 |
9,1 |
|
|
1,5 |
1,7 |
1,6 |
1,5 |
1,5 |
В последней
строке табл.5 произведен подсчет всех отношений вида (4), которые оказались
примерно одинаковыми. Поэтому неизвестную функцию ![]() аппроксимируем линейной функцией вида
(3). По формулам (5) получим:
аппроксимируем линейной функцией вида
(3). По формулам (5) получим: ![]()
Следовательно,
функция ![]() является приближенным аналитическим выражением заданной в
табл.5 неизвестной функции
является приближенным аналитическим выражением заданной в
табл.5 неизвестной функции ![]() .
.
3. Линейная аппроксимация для нелинейных функций
Часто неизвестная
функция ![]() не является линейной. Если нанести
заданные точки
не является линейной. Если нанести
заданные точки ![]() на плоскость, то по характеру их
расположения можно определить, к какому классу функций она относится. Это
делается путем сравнения полученной на плоскости картины с графиками известных
функций, которые приводятся в справочниках по математике.
на плоскость, то по характеру их
расположения можно определить, к какому классу функций она относится. Это
делается путем сравнения полученной на плоскости картины с графиками известных
функций, которые приводятся в справочниках по математике.
Для функций вида ![]() , взяв логарифм от обеих частей,
получим
, взяв логарифм от обеих частей,
получим ![]() . Обозначая теперь
. Обозначая теперь ![]() ,
получим уравнение прямой
,
получим уравнение прямой ![]() . Если исходная функция
задана точками
. Если исходная функция
задана точками ![]() , то новые точки, полученные по
правилу
, то новые точки, полученные по
правилу ![]() , будут лежать вблизи некоторой прямой вида
(3), коэффициенты которой можно найти по формула (5). Для получения неизвестных
коэффициентов
, будут лежать вблизи некоторой прямой вида
(3), коэффициенты которой можно найти по формула (5). Для получения неизвестных
коэффициентов ![]() и
и ![]() исходной
функции делаем обратные преобразования:
исходной
функции делаем обратные преобразования: ![]()
Для функции вида ![]() линейность достигается следующим образом:
линейность достигается следующим образом: ![]() . Новые точки получают по правилу (
. Новые точки получают по правилу (![]() ). Обратные преобразования – как и для
предыдущей функции.
). Обратные преобразования – как и для
предыдущей функции.
С функцией ![]() получаем:
получаем: ![]()
![]()
![]()
![]()
![]() . Точки прямой получаем по правилу (
. Точки прямой получаем по правилу (![]() ).
).
Для функции ![]() , где n – некоторое неизвестное целое число, поступают так:
, где n – некоторое неизвестное целое число, поступают так: ![]() . Новые точки вычисляются по правилу
(
. Новые точки вычисляются по правилу
(![]() ).
).
После преобразований
точек (![]() ) к точкам (
) к точкам (![]() ) необходимо проверить, лежат ли
последние вблизи прямой. Это можно делать по правилу (4). Если постоянства не
наблюдается, – значит, либо имеются ошибки при преобразовании точек, либо
неверно выбран класс функции и его следует уточнить.
) необходимо проверить, лежат ли
последние вблизи прямой. Это можно делать по правилу (4). Если постоянства не
наблюдается, – значит, либо имеются ошибки при преобразовании точек, либо
неверно выбран класс функции и его следует уточнить.
Пример 2. Для неизвестной функции ![]() , заданной в точках
, заданной в точках ![]() найти
в табл.6 ее приближенное аналитическое выражение.
найти
в табл.6 ее приближенное аналитическое выражение.
Решение.
Таблица 6
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
-1 |
0 |
1 |
2 |
2,5 |
3 |
3,5 |
4 |
5 |
|
|
0,06 |
0,13 |
0,25 |
0,52 |
0,71 |
1,02 |
1,41 |
2,01 |
3,97 |
|
|
0,1 |
0,1 |
0,3 |
0,4 |
0,6 |
0,8 |
1,2 |
2,0 |
0 |
|
|
-1 |
0 |
1 |
2 |
2,5 |
3 |
3,5 |
4 |
5 |
|
|
-2,81 |
-2,04 |
-1,39 |
-0,65 |
-0,34 |
0,02 |
0,34 |
0,70 |
1,37 |
|
|
0,8 |
0,7 |
0,7 |
0,6 |
0,7 |
0,6 |
0,7 |
0,7 |
0 |
Из табл.6 видно, что
отношения ![]() неодинаковы, – следовательно, непосредственная линейная
аппроксимация неприемлема.
неодинаковы, – следовательно, непосредственная линейная
аппроксимация неприемлема.
Анализируя график функции
![]() , построенный по точкам (
, построенный по точкам (![]() ),
), ![]() , можно заключить, что эта функция
вида
, можно заключить, что эта функция
вида ![]() (см. рис. 3, стр. 47).
(см. рис. 3, стр. 47).
Преобразуем эту функцию к
линейному виду ![]() . Обозначая
. Обозначая ![]() ,
,![]() , получаем уравнение прямой
, получаем уравнение прямой ![]() . В табл.6 приведены преобразованные точки
(
. В табл.6 приведены преобразованные точки
(![]() ) и рассмотрены отношения
) и рассмотрены отношения ![]() , которые для всех
, которые для всех ![]() приблизительно одинаковы. Следовательно,
точки (
приблизительно одинаковы. Следовательно,
точки (![]() ),
), ![]() лежат вблизи прямой
лежат вблизи прямой ![]() , коэффициенты которой получим по формулам
(5):
, коэффициенты которой получим по формулам
(5): ![]() ;
; ![]() =0,69. Произведем обратные
преобразования и получим:
=0,69. Произведем обратные
преобразования и получим: ![]() 2,99
2,99![]() ,
, ![]()
![]() .
.
Следовательно, функция ![]() является приближенным аналитическим
выражением заданной в табл.6 функции
является приближенным аналитическим
выражением заданной в табл.6 функции ![]() .
.
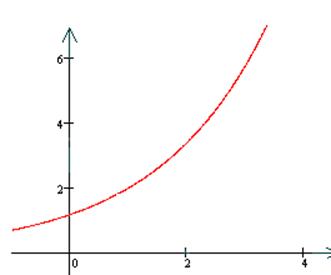 |
Рис.3.
При расчетах коэффициентов ![]() и
и ![]() рекомендуется
расширить табл.6 строками для вычислений величин
рекомендуется
расширить табл.6 строками для вычислений величин ![]() и
и ![]() . Суммы по строкам
. Суммы по строкам ![]()
![]() ,
, ![]() , получаемые непосредственно из
таблиц, облегчат вычисления по формулам (5).
, получаемые непосредственно из
таблиц, облегчат вычисления по формулам (5).
Вопросы для самоконтроля
1. Сформулируйте задачу построения наилучшего приближения на абстрактном языке.
2. К чему сводится задача построения интерполяционного многочлена с узлами интерполяции, соответствующими корням ортогонального многочлена?
3. В чем заключаются необходимые и достаточные условия того, чтобы многочлен являлся многочленом наилучшего равномерного приближения для непрерывной функции?
4. К чему сводится задача решения многомерных задач?
5. Каким образом может достигаться повышение качества приближения?
Ч.1.7. Нахождение собственных чисел и векторов матриц
методом Крылова
1.
Отыскание
собственных значений матрицы. Число ![]() называется собственным
значением матрицы А, если существует ненулевой вектор х, удовлетворяющий
уравнению
называется собственным
значением матрицы А, если существует ненулевой вектор х, удовлетворяющий
уравнению
![]() (1) и называемый собственным вектором матрицы А, отвечающий собственному
значению
(1) и называемый собственным вектором матрицы А, отвечающий собственному
значению ![]() . Запишем систему (1) в виде
. Запишем систему (1) в виде
![]() .
.
Эта однородная система имеет ненулевое решение х тогда и только тогда, когда определитель матрицы системы равен нулю, т. е.
![]() .
(2)
.
(2)
Раскрытие этого уравнения приводит к так называемому характеристическому (векторному) уравнению
![]() ,
(3) представляющему собой алгебраическое
уравнение степени n.
Решать уравнение можно любым методом для решения алгебраических и трансцендентных
уравнений. Использование теоремы Гамильтона — Кэли для матрицы A[6] приводит к системе
,
(3) представляющему собой алгебраическое
уравнение степени n.
Решать уравнение можно любым методом для решения алгебраических и трансцендентных
уравнений. Использование теоремы Гамильтона — Кэли для матрицы A[6] приводит к системе
![]() (4) где
(4) где ![]() и
и ![]() – произвольный начальный вектор.
– произвольный начальный вектор.
Если матрица А симметричная, то все
ее собственные значения являются вещественными числами. Для несимметричных
матриц возможно наличие комплексных собственных значений вида ![]() с ненулевой мнимой
с ненулевой мнимой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.