Федеральное агентство по образованию
Государственное общеобразовательное учреждение высшего профессионального образования
Амурский государственный университет
(ГОУ ВПО «АмГУ»)
Кафедра ИиУС
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА
на тему: метод Крылова по дисциплине: Вычислительная математика вариант: 21
Исполнитель студент группы 855 В.И. Колотий
Руководитель доцент И.М. Акилова
Благовещенск 2009
Задание № 1.
Дано:
![]()
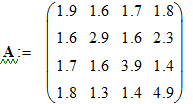
В качестве вектора с0 возьмем
|
|
|
|
|
|
|
1 |
1.9 |
12.3 |
102.092 |
865.3432 |
|
0 |
1.6 |
14.54 |
124.16 |
1055.4356 |
|
0 |
1.7 |
14.94 |
125.82 |
1064.2136 |
|
0 |
1.8 |
16.7 |
143.788 |
1225.8828 |
Тогда получим таблицу значений:
Составим систему уравнений для определения коэффициентов характеристического многочлена:
|
|
![]()
|
|
|
|
|
Решая систему методом Гаусса, найдем корни уравнения:
p1= -13.6, p2= 50.66, p3= -64.66, p4= 22.844
Таким образом, характеристический многочлен примет вид:
![]()
Решаем полученное уравнение при помощи метода Ньютона, предварительно отделив корни. Находим:
![]()
![]()
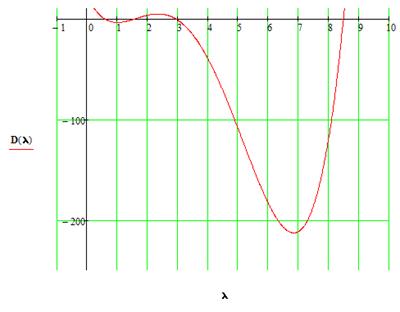
Составим таблицу знаков функции D(λ):
|
λ |
-∞ |
1 |
2 |
3 |
+∞ |
|
Sign D(λ) |
+ |
- |
+ |
- |
+ |
Из таблицы видно, что уравнение имеет четыре действительных корня:
![]() ;
;![]() ;
;![]() ;
; ![]() .
.
1. Уточним первый корень на промежутке![]() , для этого вычислим
значения функции D(λ) в
некоторых точках промежутка:
, для этого вычислим
значения функции D(λ) в
некоторых точках промежутка:
|
|
Корень содержится внутри промежутка [0;1].
Уточнение корня производим методом касательных по формуле: 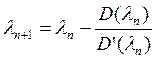 .
.
Для выбора начального приближения λ0 определим знак второй производной D”( λ) в промежутке [0;1]; имеем D”( λ)= 12λ2-81.6 λ-101,32.
D”( λ)>0
при ![]() , значит, λ0=0
, значит, λ0=0
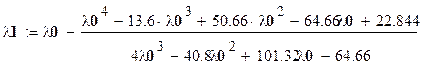
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
Следовательно, собственное число ![]() .
.
2. Уточним второй корень на промежутке![]() , для этого вычислим
значения функции D(λ) в
некоторых точках промежутка:
, для этого вычислим
значения функции D(λ) в
некоторых точках промежутка:
|
|
![]()
Корень содержится внутри промежутка [1;2].
Уточнение корня производим методом касательных по формуле: 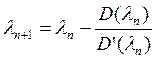 .
.
Для выбора начального приближения λ0 определим знак второй производной D”( λ) в промежутке [1;2]; имеем D”( λ)= 12λ2-81.6 λ-101,32.
D”( λ)<0
при ![]() , значит, λ0=2
, значит, λ0=2
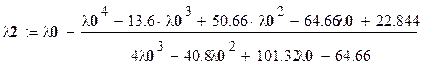
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
Следовательно, собственное число ![]() .
.
3. Уточним второй корень на промежутке![]() , для этого вычислим
значения функции D(λ) в
некоторых точках промежутка:
, для этого вычислим
значения функции D(λ) в
некоторых точках промежутка:
|
|
|
|
Корень содержится внутри промежутка [2;3].
Уточнение корня производим методом касательных по формуле: 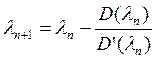 .
.
Для выбора начального приближения λ0 определим знак второй производной D”( λ) в промежутке [2;3]; имеем D”( λ)= 12λ2-81.6 λ-101,32.
D”( λ)<0
при ![]() , значит, λ0=3
, значит, λ0=3

![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
Следовательно, собственное число ![]() .
.
4. Уточним четвертый корень на промежутке [3;+∞), для этого вычислим значения функции D(λ) в некоторых точках промежутка:
|
|
|
|
Корень содержится внутри промежутка [3;+∞).
Уточнение корня производим методом касательных по формуле: 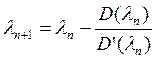 .
.
Для выбора начального приближения λ0 определим знак второй производной D”( λ) в промежутке [2;3]; имеем D”( λ)= 12λ2-81.6 λ-101,32.
D”( λ)>0
при ![]() , значит, λ0=8
, значит, λ0=8
|
|
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
Следовательно, собственное число ![]() .
.
След матрицы: 1.9+2.9+3.9+4.9+1=13.6
Сумма собственных чисел: 0.5718+1.6078+2.9248+8.4956=13.6.
Задание №2.
Дано:
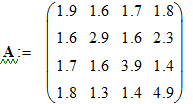
![]()
![]()
![]()
![]()
![]()
![]()
1.
![]()
Положим что ![]()
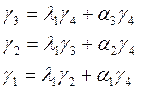
Подставим значения:
![]()
![]()
![]()
Собственный вектор матрицы определяется по формуле:
![]() ;
;
Подставляя
значения, находим 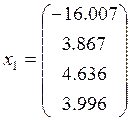
Произведём проверку:
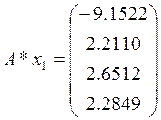
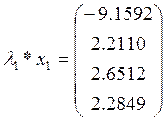
2.
![]()
Положим что ![]()
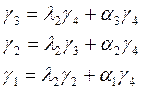
Подставим значения:
![]()
![]()
![]()
Подставляя
значения, находим 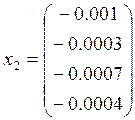
Произведём проверку:
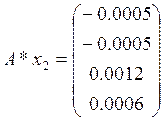
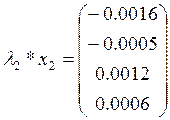
3.
![]()
Положим что ![]()
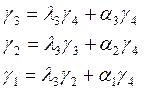
Подставим значения:
![]()
![]()
![]()
Подставляя
значения находим 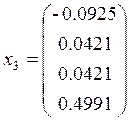
Произведём проверку:
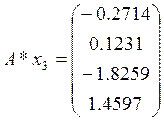

4)
![]()
Положим что ![]()
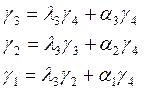
Подставим значения:
![]()
![]()
![]()
Подставляя значения находим 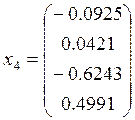
Произведём проверку
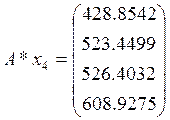
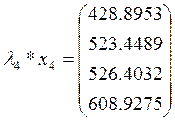
Собственные вектора матрицы А:
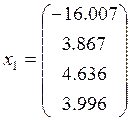 ,
,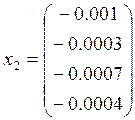 ,
,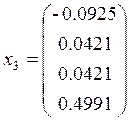 ,
,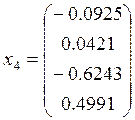
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.