Метод Галеркина. Численное решение уравнений с частными производными и интегральных уравнений

условий (6), (7) следует, что эта функция удовлетворят краевым условиям (2).

Рассмотрим выражение, называемое невязкой:

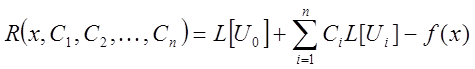                                      (9)

Выберем коэффициенты  таким образом, чтобы значение интеграла от квадрата невязки

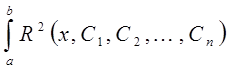                                                                                         (10)

было наименьшим.

Это достигается лишь в том случае, если невязка  ортогональна ко всем базисным функциям .

Запишем условие ортогональности:

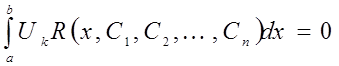
            , или

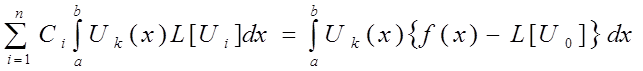       (11)

Таким образом, получена система линейных алгебраических уравнений относительно коэффициентов .

В качестве базисных функций можно выбрать линейные комбинации функций из этой системы. Достаточно  лишь, чтобы выбранные функции были линейно независимы на отрезке[a,b].

Пример 1. Методом Галеркина найти приближенное решение уравнения     , удовлетворяющее краевым условиям

Решение. Выберем в качестве системы базисных функций  следующие тригонометрические функции:

 

Эти функции линейно независимы на отрезке , причем функция  удовлетворяет краевому условию, а остальные – нулевым краевым условиям:

Приближенное решение задачи ищем в виде

.

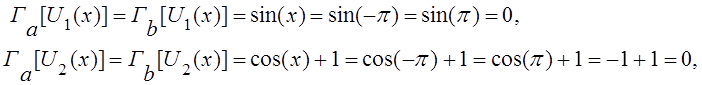
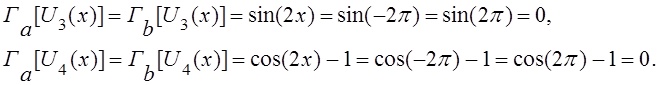
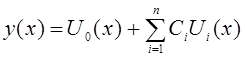Находим

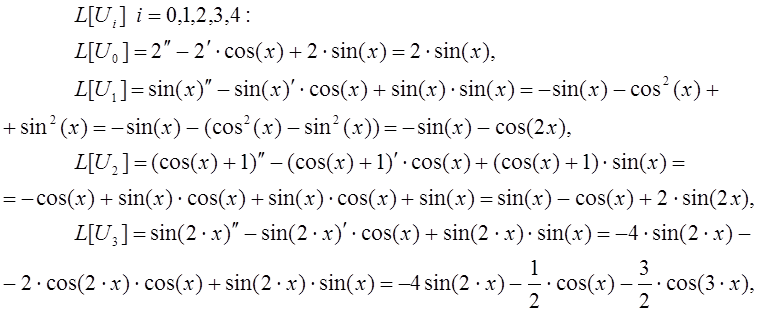
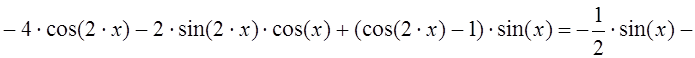
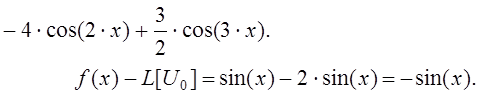
Вычисляем коэффициенты системы (11), пользуясь следующими обозначениями:

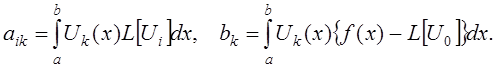
Учитывая при этом ортогональность системы тригонометрических функций, имеем:

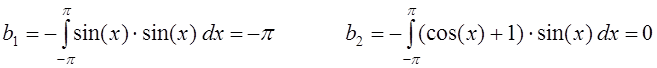
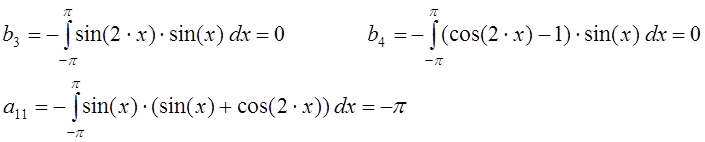
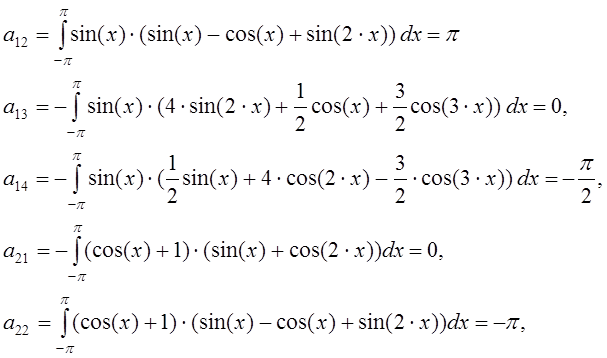
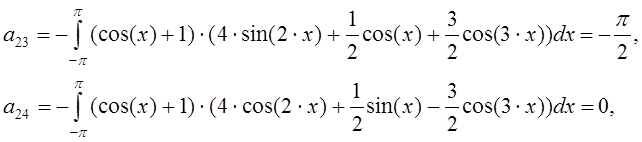
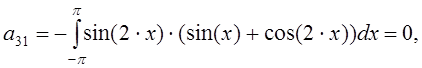
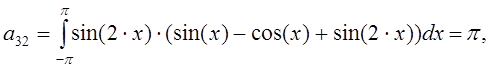
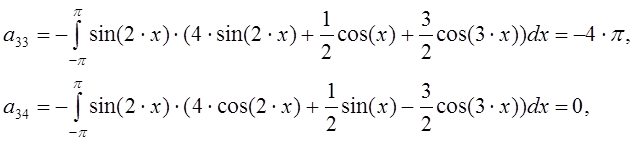
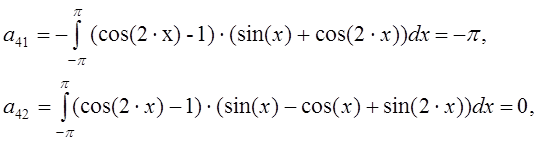
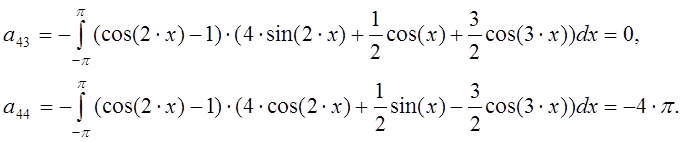
Составим систему линейных алгебраических уравнений

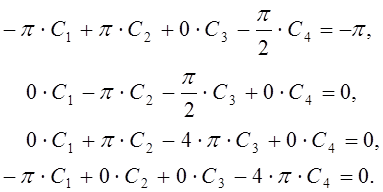
Произведя соответствующие сокращения, приходим к системе

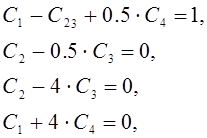
из которой получаем

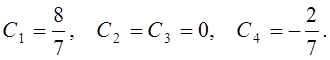
Таким образом, имеем:

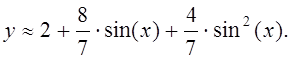
Пример 2. Методом Галеркина найти приближенное решение уравнения: , удовлетворяющее краевым условиям  .

Решение.  В качестве системы базисных функций ,  выберем следующие функции:

  

Они независимы и  удовлетворяют нулевым  краевым условиям.

Приближенное решение задачи ищем в виде

Подставляя y в левую часть исходного уравнения, получаем невязку

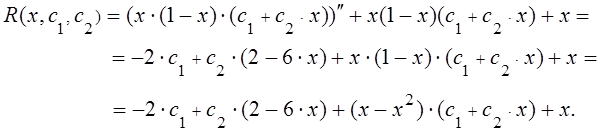
Учитывая ортогональность функции R к функциям и , получаем систему.

Первое уравнение системы:

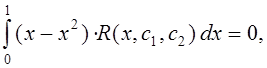
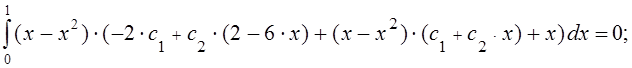
второе уравнение системы:

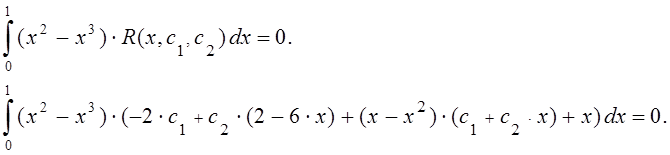
Вычислив интегралы, получим систему линейных алгебраических уравнений для определения коэффициентов  и :

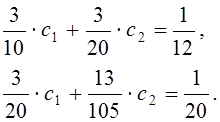
Решая эту систему, получим

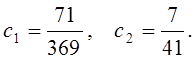
Таким образом: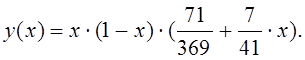 

Вопросы для самоконтроля

1.  Каким условиям должна удовлетворять система базисных функций?

2.  Когда система базисных функций является полной?

3.  Когда система базисных функций является ортогональной?

4.  Каким условиям должна удовлетворять функция ?

5.  Какое выражение называется невязкой?

6.  Каким образом выбираются коэффициенты ?

Ч.1.12. Численное решение уравнений с частными  производными и интегральных уравнений

1. Метод сеток

Метод сеток, или метод конечных разностей, – один из самых распространенных в настоящее время методов численного решения уравнений с частными производными. В его основе лежит идея замены производных конечно-разностными  отношениями.          

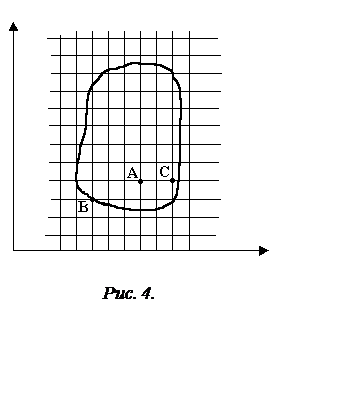Будем  рассматривать лишь случай двух независимых переменных. Пусть в плоскости  имеется некоторая область  с границей (рис. 4). Построим на плоскости два семейства параллельных прямых:                                                                                  

   ,                 

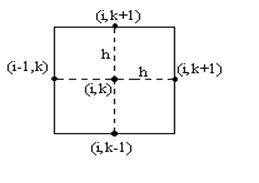
Точки пересечения этих прямых назовем узлами. Два узла называются соседними, если они удалены друг от друга в направлении оси или  на расстояние, равное шагу сетки h или l соответственно. Выделим узлы, принадлежащие области , а также некоторые, не принадлежащие этой области, но расположенные на расстоянии меньше  чем шаг от границы . Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству, называются внутренними (узел , рис. 4), оставшиеся из выделенных узлов называются граничными (узлы , рис. 4).

Значения искомой функции  в узлах сетки будем обозначать через  . В каждом внутреннем узле  заменим частные производные разностными отношениями:

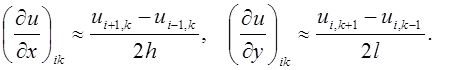                                           (1.1)

В граничных точках приходится пользоваться менее точными формулами вида:

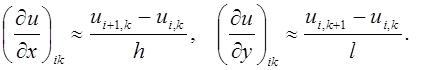                                               (1.2)

Аналогично заменяются частные производные второго порядка, – например:

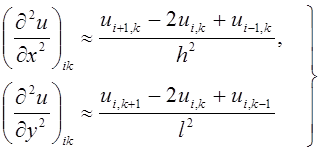                                                                  (1.3)

Указанные замены производных в каждом узле сетки позволяют свести решение уравнений с частными производными к решению системы разностных уравнений.

2. Метод сеток для задачи Дирихле

Первая краевая задача, или задача Дирихле, для уравнения Пуассона

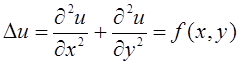                                                                              (2.1)

ставится следующим образом: найти функцию , удовлетворяющую внутри некоторой области  уравнению (4), а на границе  –   условию

,                                                                                                 (2.2)

где – заданная непрерывная функция. Выбрав шаги  и l по x и y соответственно, строим сетку

                                                                

                     

и заменяем в каждом внутреннем узле  производные 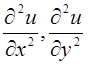 конечно- разностными отношениями (1.3), а уравнение (2.1) – конечно-разностными уравнениями

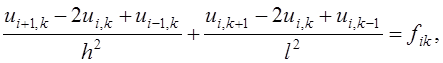                                             (2.3)

где .

Уравнения (2.3) вместе со значениями  в граничных узлах образуют систему линейных алгебраических уравнений относительно значений функции в узлах . Наиболее простой вид эта система имеет для прямоугольной области и для l=h. В таком случае уравнения (2.3) записываются следующим образом:

,                                                    (2.4)

а значения в граничных узлах в точности равны значениям граничной функции. При  уравнение (2.1) называется уравнением Лапласа, а соответствующие конечно-разностные уравнения имеют вид:

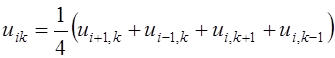.                                                             (2.5)

При составлении уравнений (2.4) и (2.5) была использована схема узлов, изображенная  на рис. 5.  Иногда  бывает  удобнее  использовать схему узлов,                               

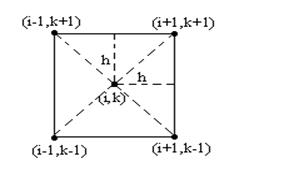Рис. 5.                                                      Рис. 6.   

показанную на рис. 6.  В этом случае уравнению Лапласа соответствуют следующие конечно-разностные уравнения:

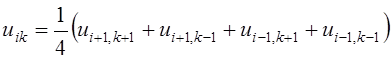,                                                    (2.6)

а для уравнения Пуассона будем иметь

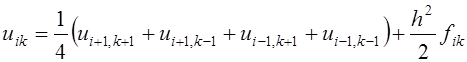.                                       (2.7)

Погрешность замены дифференциального уравнения разностными, т.е. остаточный член для уравнения Лапласа, оценивается неравенством