Анализ результатов уравнивания (Глава 3 дипломного проекта)

3. АНАЛИЗ РЕЗУЛЬТАТОВ УРАВНИВАНИЯ

3.1. Допуски

3.1.1. Невязки

Введем обозначения

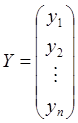       - случайный вектор

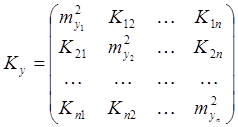     - корреляционная матрица вектора Y.

где    - квадрат средних квадратических ошибок,

- корреляционные моменты     и   .

Если ввести вектор математических ожиданий

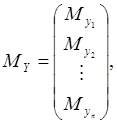
то корреляционная матрица вектора Y будет записана в следующем виде

Сформулируем обобщенную теорему оценки точности.

Если случайный вектор Y есть линейная функция вектора Х,

где А и А₀ – матрицы с постоянными элементами, то

                                                                                       (115)

где K_y и K_x – корреляционные матрицы векторов Y и X соответственно.

Получим корреляционную матрицу результатов измерений.

Пусть

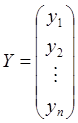         -  вектор результатов измерений.

Так как измерения независимы, К_ij = 0.

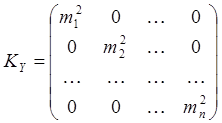
- корреляционная матрица результатов измерений.

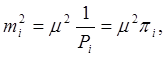
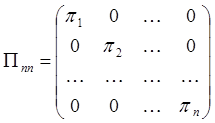
-   матрица обратных весов результатов измерений.

В итоге  корреляционную матрицу результатов измерений можно представить в виде

                                                                                         (116)

Получим корреляционную матрицу невязок.

Условные уравнения поправок имеют вид

,                                                                                          (117)

где   

- вектор поправок равен разности между векторами уравненных  (  ) и измеренных (  ) величин.

Если вектор V в уравнении (117) заменить вектором истинных поправок

то равенство не нарушается,

                                                                                          (118)

Отсюда выразим вектор невязок

, где       -   постоянная величина.

Применяя к вектору W обобщенную теорему оценки точности (115), получим корреляционную матрицу невязок

или

                                                                                           (119)

Развернем левую и правую части выражения (119)

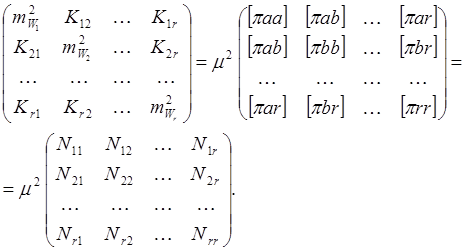                               (120)

На основании (120)

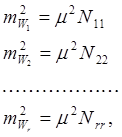
где   - квадратичные коэффициенты (диагональные элементы) матрицы коэффициентов нормальных уравнений.

Допустимое значение невязки

или

                                                                                (121)

где - аргумент интеграла вероятностей       (предполагается нормальный закон распределения результатов измерений).

b - доверительная вероятность.

m- средняя квадратическая ошибка единицы веса.

При уравнивании геодезических сетей поиск и отбраковку грубых ошибок измерений осуществляют по допустимым значениям невязок.

Рассчитываем   допустимые значения невязок  для модели нивелирной сети представленной на рисунке , а потом сравним с  . Если             , то невязки в допуске, то есть грубых ошибок нет.

Примем аргумент интеграла вероятностей       что соответствует доверительной вероятности   

Средняя квадратическая ошибка единицы веса, полученная по результатам уравнивания       

По первому полигону получена невязка   см. Вычислим допустимое значение невязки первого полигона

 см.

Невязка первого полигона в допуске

.

По второму полигону получена невязка   см. Вычислим допустимое значение невязки второго полигона

 см.

Невязка второго полигона в допуске

По третьему полигону получена невязка  см. Вычислим допустимое значение невязки третьего полигона

 см.

Невязка третьего полигона в допуске

По четвертому полигону получена невязка   см. Вычислим допустимое значение невязки четвертого полигона

 см.

Невязка четвертого полигона в допуске

Все невязки находятся в допуске, т.е. соблюдается условие .                    На основании этого можно сделать вывод, что  грубые ошибки измерений в сети отсутствуют.

3.1.2. Поправки

Выразим вектор поправок V из коррелатного уравнения поправок

                                                                                           (122)

Применим к этому уравнению обобщенную теорему оценки точности (115)

  - корреляционная матрица коррелат.

Для определения    представим вектор коррелат как решение системы нормальных уравнений методом обращения

                                                                                          (123)

Тогда

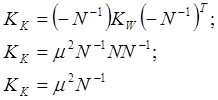                                                                        (124)

- корреляционная матрица вектора коррелат, где

- обратная матрица системы нормальных уравнений.

После этого получим  корреляционную матрицу вектора поправок

или

                                                                             (125)

где

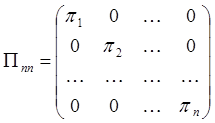
-  матрица обратных весов результатов измерений;

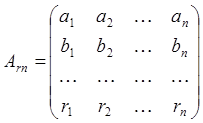
- матрица коэффициентов условных уравнений поправок ;

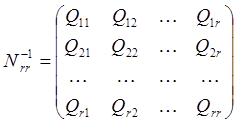
- обратная матрица системы нормальных уравнений.

Рассмотрим вычисление корреляционной матрицы поправок нивелирной сети и допуски для поправок МНК. Допустимые значения поправок можно использовать наряду с невязками для отбраковки грубых ошибок измерений.

                                                                                         (126)

 - диагональный элемент корреляционной матрицы поправок.

По этой формуле вычисляются допустимые поправки для коррелатного способа уравнивания нивелирной сети.

Для параметрического способа корреляционная матрица поправок вычисляется по следующей формуле