Анализ результатов уравнивания (Глава 3 дипломного проекта), страница 2

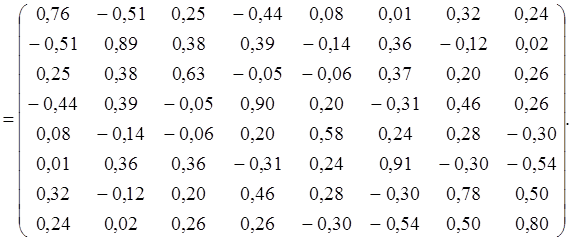
                                                                                        (127)

- корреляционная матрица уравненных результатов измерений, где

- корреляционная матрица результатов измерений.

Допустимые поправки вычисляются по следующей формуле

где - аргумент интеграла вероятностей равный 2.5 для .

-средняя квадратическая ошибка поправок, которая вычисляется по формуле

где    - обратный вес результата измерения;

- диагональные элементы матрицы весовых коэффициентов уравненных результатов измерений

Если выполняется условие , то можно считать, что в данном измерении грубая ошибка отсутствует.

Рассчитаем  v_iдоп    для нивелирной сети на рисунке , а потом сравним с  v_i .

Найдем    

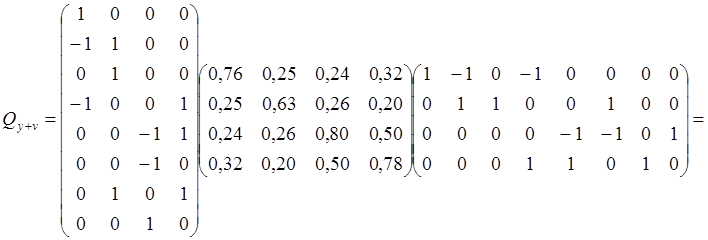
Для первого превышения получена поправка см. Вычислим допустимое значение поправки первого превышения  

см.

Поправка первого  превышения в допуске

Для второго превышения получена поправка см. Вычислим допустимое значение поправки второго превышения

см.

Поправка второго превышения в допуске

Для третьего превышения получена поправка см. Вычислим допустимое значение поправки  третьего превышения

см.

Поправка третьего превышения в допуске

Для четвертого превышения получена поправка см. Вычислим допустимое значение поправки четвертого превышения

см.

Поправка четвертого превышения в допуске

Для пятого превышения получена поправка см. Вычислим допустимое значение поправки  пятого превышения

см.

Поправка пятого превышения в допуске

Для шестого превышения получена поправка см. Вычислим допустимое значение поправки шестого превышения

см.

Поправка шестого превышения в допуске

Для седьмого превышения получена поправка см. Вычислим допустимое значение поправки  седьмого превышения

см.

Поправка  седьмого превышения в допуске

Для восьмого превышения получена поправка см. Вычислим допустимое значение поправки восьмого превышения

см.

Поправка восьмого превышения в допуске

На основании этих расчетов можно сделать вывод: все поправки находятся в допуске, а значит грубые ошибки измерений в сети отсутствуют.

3.2. Корреляционный анализ ошибок и поправок

Выполним корреляционный анализ истинных ошибок  модели нивелирной сети и поправок , полученных из уравнивания по методу наименьших квадратов с целью установить степень компенсации ошибок измерений поправками МНК.

Коэффициент корреляции  является мерой тесноты линейной корреляционной зависимости, максимальные значения +1 он принимает в случае функциональной прямолинейной зависимости. Равенство = 0 говорит об ее отсутствии. Если > 0, то существует положительная корреляционная зависимость, при которой увеличение аргумента вызывает увеличение математического ожидания функции. Если < 0, то имеет место отрицательная корреляционная зависимость, когда с увеличением аргумента математическое ожидание функции уменьшается.

На практике математическое ожидание случайных величин Х и Y, коэффициент корреляции , среднее квадратическое отклонение случайных величин X и Y,  и  неизвестны, поэтому определяют их оценки по n наблюдаемым парам. Запишем основные формулы.

Среднее арифметическое значений случайной величины Х

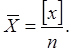
Среднее арифметическое значений случайной величины Y

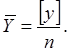
Уклонение от среднего значения случайной величины Х

Уклонение от среднего значения случайной величины Y

Оценка среднего квадратического отклонения случайной величины Х

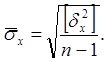
Оценка среднего квадратического отклонения случайной величины Y

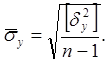
Оценка коэффициента корреляции

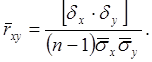
Для оценки значимости коэффициента корреляции используют специальную функцию, называемую функцией Фишера

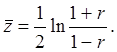
Величина   может быть вычислена по таблицам /8/.

Оценка среднего квадратического отклонения

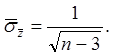
Доверительный интервал для

где   - доверительная вероятность (для  b = 0,988 ,   t_b= 2,5).

Доверительный интервал для r

Если    , то связь Х и У установлена.

В качестве случайных величин Х возьмем истинные погрешности измерений D_i , а вместо Y – поправки v, полученные при уравнивании нивелирной  сети. Для удобства все вычисления поместим в таблице 11.

Табл. 11

Корреляционный анализ

å                 -3,5                         1,81                        0,02                       -0,03

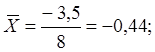
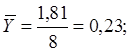
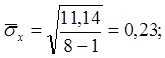
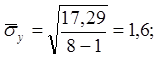
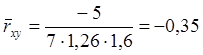
-коэффициент корреляции ошибок и поправок;

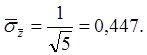
взяли из таблицы. = 0,365.

Рассчитаем границы доверительного интервала для функции z

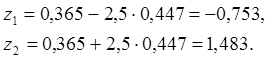
По значению  и  в таблицах /6/ находим границы доверительного интервала для коэффициента корреляции

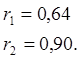
Таким образом, длина доверительного интервала для коэффициента корреляции  составила

Так как , то корреляционная связь между случайными величинами Х и Y установлена.

Таким образом, для модели нивелирной сети заданной конструкции установлено наличие линейной корреляционной связи между ошибками измерений и поправками МНК.