Математическое моделирование биологических процессов: Учебное пособие

МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Государственное высшее учебное заведение

Гомельский государственный медицинский институт

Кафедра медицинской и биологической физики

Математическое моделирование

биологических процессов

Учебное пособие

 

Гомель, 2003 г.

Тема:  Математическое моделирование биологических

процессов

Лабораторная работа 1

Математическое моделирование биологических процессов.

Моделирование функционирования сердечно-сосудистой

системы

Время занятия – 135 минут.

Цель: Изучить современные модели сердечно-сосудистой системы и показать на их примере эффективность применения метода моделирования для оценки состояния и выявления характерных особенностей поведения сложных биологических объектов.

1.1.  Вопросы теории

1.1.1. Математическое моделирование биологических процессов. Биофизика сложных систем.

Функционирование сложной биологической системы, в том числе сердечно-сосудистой системы, является результатом взаимодействия составляющих ее элементов и протекающих в ней процессов. Следует иметь в виду, что согласно общему принципу восходящей иерархии типов движения (механическое – физическое – химическое – биологическое – социальное), биологическая форма движения не может быть полностью сведена к механической, физической или химической форме движения, а биологические системы не могут быть полностью описаны с позиций какой-либо одной из этих форм движения. Эти формы движения могут служить моделями биологической формы движения, то есть ее упрощенными  образами.

Выяснить основные принципы регулирования процессов сложной биологической системы можно с помощью построения сначала механической, физической или химической  модели системы, а затем построения их математических моделей, то есть отыскания описывающих эти модели математических функций, в том числе уравнений (создания математических моделей). Чем ниже уровень иерархии – тем проще модель, тем больше факторов реальной системы исключаются из рассмотрения.

Моделирование – это метод, при котором производится замена изучения некоторого сложного объекта (процесса, явления) исследованием его упрощенного аналога - модели. В биофизике, биологии и медицине широко применяются физические, химические, биологические и математические модели. Например, течение крови по сосудам моделируется движением жидкости по трубам (физическая модель). Биологическая модель – это простые биологические объекты, удобные для экспериментального исследования, на которых изучают свойства реальных более сложных биологических систем. Например, закономерности возникновения и распространения потенциала действия по нервному волокну были изучены на биологической модели – гигантском аксоне кальмара.

Математическая модель – это совокупность математических объектов и отношений между ними, отражающая интересующие исследователя свойства и характеристики реального объекта. Адекватную математическую модель можно построить только с привлечением конкретных данных и представлений о механизмах сложных  процессов. После построения математическая модель «живет» по своим внутренним законам,  познание которых позволяет выявить характерные черты исследуемой системы (см. схему на рис. 1.1.). Результаты моделирования составляют основу управления процессами любой природы.

Биологические системы, по сути, являются чрезвычайно сложными структурно-функциональными единицами.

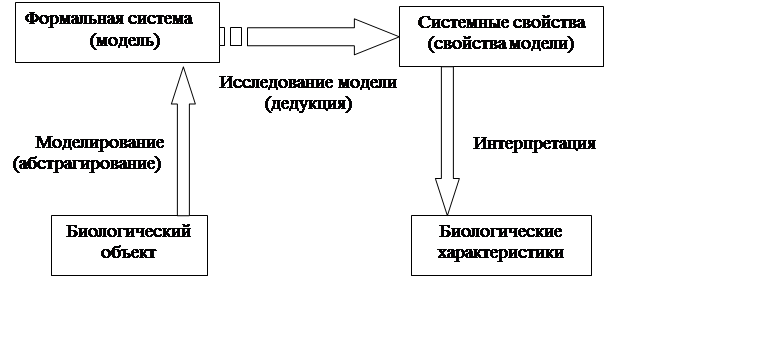
Рис. 1.1. Схема системного подхода в моделировании биологического объекта.

Чаще всего математические модели биологических процессов задаются в виде дифференциальных или разностных уравнений, но возможны и другие типы представлений модели. После того как модель построена, задача сводится к изучению ее свойств методами математической дедукции или путем машинного моделирования.

При изучении сложного явления обычно предлагают несколько альтернативных  моделей. Проверяют качественное  соответствие этих моделей объекту. Например, устанавливают наличие устойчивых стационарных состояний в модели, существование колебательных режимов.  Модель, наилучшим образом соответствующую исследуемой системе, выбирают в качестве основной.  Выбранную модель уточняют применительно к конкретной исследуемой системе. Задают числовые значения параметров по экспериментальным  данным.

Процесс поиска математической модели сложного явления можно разделить на этапы, последовательность и взаимосвязь которых отражает схема ни рис. 1.2.

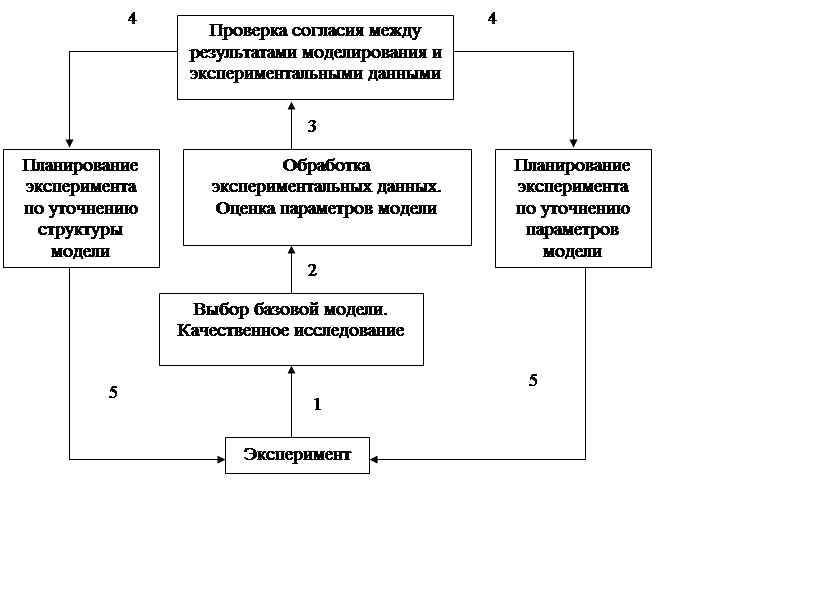
Рис. 1. 2. Схема  поиска математической модели.

          Этап 1 соответствует сбору имеющихся к началу исследования данных об изучаемом объекте. 

На этапе 2 осуществляется выбор базовой модели (системы уравнений) из возможных альтернативных моделей по качественным признакам. 

На этапе 3 производится идентификация параметров модели по экспериментальным данным. 

На этапе 4 осуществляется  проверка поведения модели на независимых экспериментальных данных. Для этого часто приходится ставить дополнительные эксперименты.

Если взятые для верификации модели экспериментальные данные «не вписываются» в модель, требуется проанализировать ситуацию и выдвинуть иные модели, исследовать свойства этих новых моделей, а затем поставить эксперименты, позволяющие сделать вывод о предпочтительности одной из них (этап 5).