Физика \ Медицинская и биологическая физика

Математическое моделирование биологических процессов: Учебное пособие, страница 3

1.1.2. Модели функционирования сердечно-сосудистой системы

1.1.2.1. Модель О. Франка.

С позиции механики, точнее, гидродинамики, сердечно-сосудистую систему можно представить как совокупность следующих элементов:

1)  ритмически работающий насос (сердце),

2)  камера стабилизации давления (аорта и крупные артерии),

3)  камера сопротивления (периферические сосуды),

4)  камера распределения крови в тканях (капиллярная сеть),

5)  камера емкости (венозный сосудистый отрезок).

Одной из первых моделей сердечно-сосудистой системы, построенной на основе таких представлений, является модель О. Франка (1899 г.).

В модели О. Франка система крупных сосудов артериальной части большого круга кровообращения моделируется одной упругой камерой, а система мелких сосудов – жесткой трубкой. Сердце представляется механическим насосом, соединенным с упругой камерой клапаном (рис.1. 6).

Работая в рамках модели О. Франка, можно найти формулу для оценки ударного объема крови - одного из важных параметров состояния сердечно-сосудистой системы. Ударным объемом крови называют объем крови, выбрасываемый левым желудочком сердца в аорту за период систолы.

Согласно модели О. Франка, объем крови, выходящий из сердца со скоростью Q (объемная скорость) за время dt (dt®0), равен сумме изменения объема крови в упругой камере (dV) и объема крови, протекающего через жесткую трубку за время dt со скоростью Q0:

Ударный объем крови по определению равен:

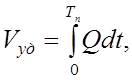
где Тп – период пульса.

 


Рис.1. 6.  Модель О. Франка.

1 – упругая камера (крупные артерии), представляющая собой цилиндр с поршнем, соединенным с упругой пружиной;

2 – жесткая трубка (периферические сосуды);

3 – клапан;

4 – насос (левый желудочек сердца).

Стрелки С и Д показывают направление поступления крови в разные части системы в период систолы и диастолы (соответственно).
 

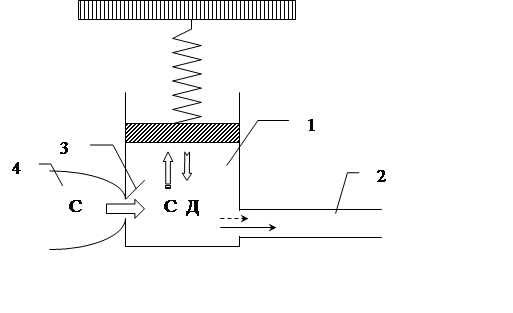
С учетом упругих свойств  крупных  сосудов и  законов движения жидкости по жесткой трубе формула для определения ударного объема крови выглядит следующим образом:

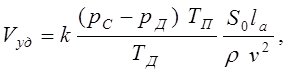                                  (1.3)

где k – коэффициент пропорциональности, введение которого связано со сделанными упрощениями; pC, pД – систолическое и  диастолическое  давления;

S0 – эффективная площадь поперечного сечения крупных артерий; lа – эффективная длина крупных артерий; TП, TД – период пульса и период диастолы соответственно; r - плотность крови; v – скорость крови.

Хотя формула (1.3) отражает основной характер зависимости ударного объема крови от вышеуказанных  параметров, однако, вследствие множества упрощений, сделанных при ее выводе, она не может использоваться для количественных расчетов в медицинской практике. Существуют также трудности в измерениях на практике некоторых параметров, входящих в формулу, что делает ее использование целесообразным только в академических целях. 

1.1.2.2.  Гидродинамическая модель движения крови по кровеносному руслу.

Можно моделировать функционирование отдельных элементов сердечно-сосудистой системы.  Рассмотрим модель движения крови по кровеносному руслу на основе законов механики. Пусть кровь по кровеносному руслу распространяется как жидкость в жесткой трубе. Кроме того, в продвижении крови по кровеносному руслу участвуют упруго деформирующиеся стенки сосудов.

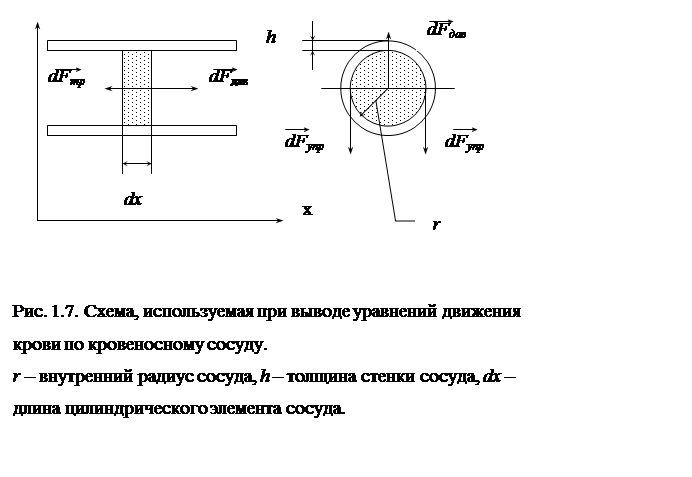
Представим кровеносный сосуд как трубку с радиусом просвета (поперечного сечения) r. Движение малого объема крови (цилиндра - радиусом r и высотой dx) (рис.1.7), описывается вторым законом Ньютона (первое уравнение системы 1.4). Давление крови внутри сосуда уравновешивается силой упругости стенок сосуда (второе уравнение системы 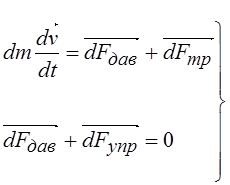1.4).

                                        (1.4)

где dm – масса объема крови, v – скорость, dFдав – сила давления, dFтр – сила вязкого трения, dFупр – сила упругости.

 


Рассмотрим первое из уравнений системы (1.4). Возьмем проекцию этого уравнения на ось x. Учтем, что

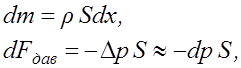
где r - плотность крови, S – площадь просвета сосуда (S=pr2), dp»Dp=p2-p1 – изменение давления на участке  dx в связи с малостью этого участка приблизительно равно дифференциалу функции давления.

Для элементарного объема крови сила трения является силой вязкого трения, которую можно рассчитать по формуле Ньютона с использованием  формулы  Пуазейля:

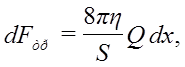
где h - вязкость крови, Q=S.v - объемная скорость крови.

Тогда первое уравнение системы (1.4) с учетом введенных величин можно записать в виде:

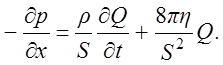
Рассмотрим второе уравнение системы (1.4).

Плоскостью, проходящей через диаметр, условно разделим рассматриваемый объем крови и прилегающие к нему стенки сосуда на две половины (рис. 1.7). Образовавшееся сечение имеет площадь 2rdx. На эту площадь действует сила давления

dFдав=p.2rdx.

Силы давления стремятся разъединить обе половинки сосуда, в результате чего в сосудистой стенке возникают силы, препятствующие этому – упругие силы:

dFупр= s .2hdx,

где s- тангенциальное напряжение в стенке сосуда, 2hdx - сумма площадей продольных сечений стенки, к которым приложены упругие силы.

dFдав=dFупр,

p2rdx=s .2hdx,

pr=sh Þ p=sh/r.

Учитывая закон Гука (ds=Edr/r, где Е – модуль упругости Юнга) и выражение площади поперечного сечения сосуда (S=pr2, dS=2prdr), найдем дифференциал функции давления:

                                               

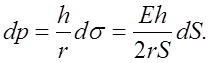
Разделим левую и правую части этого уравнения на dt и учтем, что      dS= -dQ dt/dx:

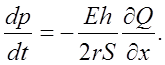
Тогда система из системы уравнений (1.4) получим систему уравнений 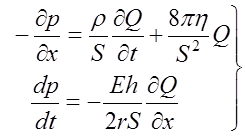(1.5):

                                        (1.5)

Система уравнений (1.5) описывает движение крови по кровеносному сосуду в рамках механического подхода. Система состоит из двух уравнений и содержит две неизвестные  (Q и р), поэтому разрешима. Решение системы уравнений (1.5) выходит за рамки нашего курса, поэтому здесь приведем лишь конечные формулы, являющиеся  решением  данной системы уравнений.

Скачать файл