Одно из решений системы (функция давления) представляет собой уравнение затухающей волны (пульсовая волна):
![]() (1.6)
(1.6)
где А0 – максимальная амплитуда давления крови, w - частота колебаний давления крови.
Коэффициент c показывает, как быстро затухает колебание по длине сосуда. Коэффициент b связан со скоростью распространения волны. Оба эти коэффициента выражаются через величины, входящие в уравнения системы (1.5).
1.1.2.3. Модель, представляющая сердечно-сосудистую систему как электрическую цепь. Общая модель
При рассмотрении динамических моделей сложных систем прослеживается закономерность поведения сложных систем, относящихся к разным областям науки: механике, физике, химии, биологии, социальным наукам. Эта закономерность вытекает из внутренней взаимосвязи элементов, составляющих сложную систему. Существуют науки, изучающие наиболее общие законы поведения и управления сложными системами: кибернетика, синергетика, диалектика и др. Нас интересует данный аспект в качестве еще одной разновидности метода моделирования. Часто можно провести аналогию между процессами явно не относящимися к одной области науки. При этом взгляд на изучаемую систему под новым углом зрения часто помогает найти новые характеристики системы, закономерности.
Рассмотрим систему уравнений (1.5), описывающую движение крови по кровеносному руслу в рамках механического подхода. Введем новые постоянные
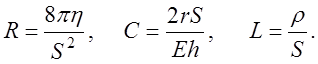
![]()
Строго говоря, параметры h, Е, S и r не постоянны, они изменяются, например, при изменении давления в сосуде. Но при определенных условиях (например, при высоких скоростях крови в аорте), можно считать эти параметры постоянными.
Тогда систему уравнений (1.5) можно записать в виде:
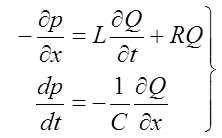 (1.7)
(1.7)
Такой же вид имеют уравнения, известные в электротехнике и описывающие изменения электрического потенциала (j) вдоль электрической цепи (∂j/∂x) и во времени (∂j/∂t). Данная электрическая цепь содержит: резистор с омическим сопротивлением R, конденсатор, емкости C, и катушку индуктивности с индуктивностью L.
Можно провести аналогию между движением крови по кровеносному руслу и протеканием электрического тока по электрической цепи.
Объемную скорость крови можно сравнить с силой электрического тока. Перепад давлений вызывает ток крови, а разность потенциалов – электрический ток. Эластичность стенок кровеносного сосуда делает участок сосуда переменной емкостью для крови. В случае электрической цепи емкостью для электрических зарядов является конденсатор. Вязкостное сопротивление движению крови по кровеносному руслу можно сравнить с омическим сопротивлением электрической цепи. И, наконец, инерционные свойства крови лежат в основе инерционной индуктивности крови, подобно тому, как электромагнитная индукция электронов лежит в основе индуктивности катушки индуктивности.
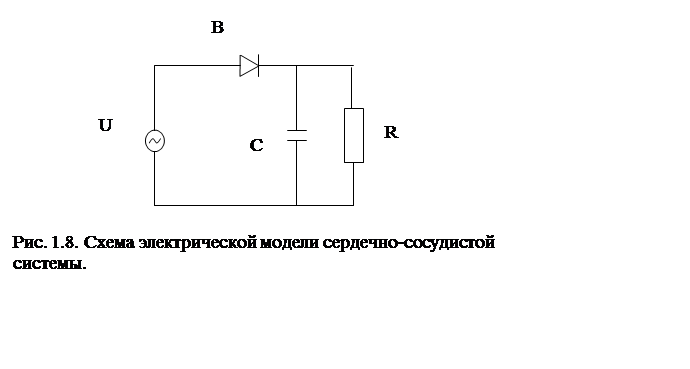
В рамках данной аналогии можно построить электрическую модель сердечно-сосудистой системы (рис. 1.8.).
Аналогом сердца в этой модели является источник несинусоидального переменного электрического напряжения (U). Сердечный клапан представляется выпрямителем тока (В). Как уже рассматривалось, упругие свойства крупных сосудов моделируются конденсатором (емкости С). А вязкостные свойства периферических сосудов – резистором (сопротивления R).
 |
1.1.2.4. Модель, представляющая сердечно-сосудистую систему как электрическую цепь. Чисто резистивная модель
Вследствие низкой способности сосудов периферической системы к расширению при изменении давления крови емкость сосудов (С) стремится к 0. Поэтому второе уравнение системы (1.7) теряет смысл. Кроме того, для периферических сосудов величина индуктивности (L) оказывается малой. Причиной этому является небольшая величина просвета артериол и капилляров по сравнению с артериями. Если пренебречь первым членом правой части первого уравнения системы (1.7), то кровоток в микрососуде описывается уравнением Пуазейля:
P1-P2=R0Q, (1.8)
где P1- P2 – разность давления крови на концах выбранного участка сосуда, R0 – периферическое сопротивление крови, Q – объемная скорость кровотока.
Это уравнение аналогично закону Ома для участка электрической цепи. Оно также справедливо для системы микрососудов в целом, и при этом Q - объёмная скорость кровотока во всей системе, а R0 - общее сопротивление системы сосудов. Если провести аналогию с электрическими цепями, то общее вязкостное сопротивление последовательно соединённых сосудов равно сумме сопротивлений отдельных сосудов. А для системы параллельно соединённых сосудов величина, обратная общему вязкостному сопротивлению, равна сумме проводимости отдельных сосудов. Уравнение Пуазейля в системе микроциркуляций называют формулой периферического гемодинамического сопротивления. Представление кровотока в системе микроциркуляции называют чисто резистивной моделью кровообращения.
1.1.2.5. Модели электрической активности сердца
Сокращение сердца представляет собой периодический процесс. Как известно, периодические сокращения сердца вызываются периодическими изменениями электрической активности возбудимых волокон сердца. Для моделирования электрической активности возбудимых волокон сердца используют генератор переменного электрического поля. Впервые эта идея была предложена голландским учёным Эйнтховеном.
Основные постулаты модели следующие:
1. Электрическое поле сердца представляется как поле точечного токового диполя с дипольным моментом Е, называемым интегральным электрическим вектором сердца (ИЭВС). Этот вектор складывается из диполей разных частей сердца.
2. ИЭВС находится в однородной изотропной проводящей среде, каковой являются ткани организма.
3. ИЭВС меняется по величине и направлению. Его начало неподвижно и находится в атриовентрикулярном узле, а конец описывает сложную пространственную кривую.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.