



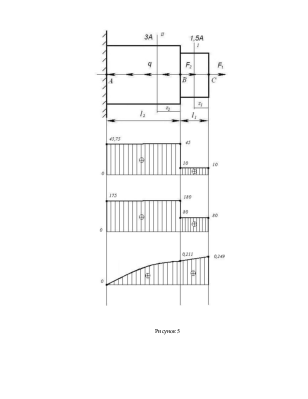








Рисунок 1
Задача №1
Для статически
определимой системы содержащей стальной стержень (рисунок 1) круглого
поперечного сечения, находящейся под действием осевых сил ![]() и
и ![]() , а так
же распределенной нагрузки q, требуется:
, а так
же распределенной нагрузки q, требуется:
1) построить в
масштабе эпюру продольных сил ![]() ;
;
2) из условия прочности определить площадь и габаритные размеры опасного сечения стержня;
3) построить в масштабе эпюру напряжений;
4) построить эпюру перемещений в масштабе при заданных соотношениях площадей сечений. Собственным весом стержня пренебречь.
Дано:
1) модуль упругости для стали принять равным ![]() ;
;
2) допускаемое напряжение ![]() ;
;
3) ![]() ;
;![]() ;
;
4) ![]() ;
; ![]() ;
; ![]() .
.
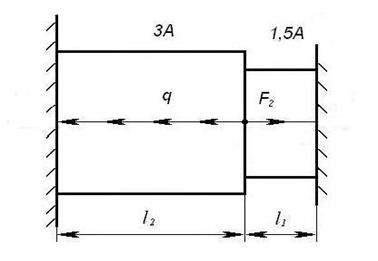
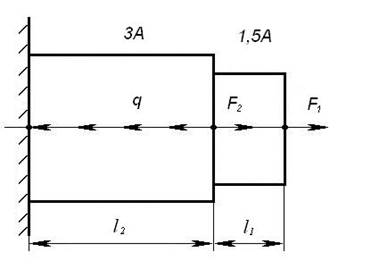
Рисунок 2
Задача №2
Для статически
неопределимой системы, содержащей стальной стержень (рисунок 2) круглого
поперечного сечения, испытывающей деформации растяжение-сжатие и находящейся
под действием осевых сил ![]() и
и ![]() , а так же распределенной нагрузки q, требуется:
, а так же распределенной нагрузки q, требуется:
1) из условия совместности деформации определить реакции опор;
2) построить в
масштабе эпюру продольных сил ![]() ;
;
3) из условия прочности определить площадь и габаритные размеры опасного сечения стержня;
4) построить в масштабе эпюру напряжений;
5) построить эпюру перемещений в масштабе при заданных соотношениях площадей сечений. Собственным весом стержня пренебречь.
Дано:
1) модуль
упругости для стали принять равным ![]() ;
;
2) допускаемое
напряжение ![]() ;
;
3) ![]() ;
;![]() ;
;
4) ![]() ;
; ![]() .
.
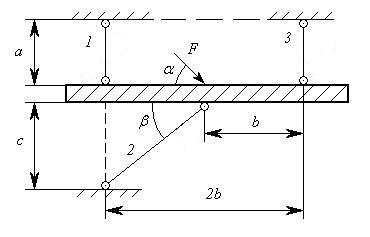
Рисунок 3
Задача №3
Для плоской стержневой системы, содержащей 3 стержня, которые удерживают некоторый брус нулевой толщины, к которому приложена внешняя сосредоточенная сила F (рисунок 3), требуется:
1) определить реакции связей, действующие в стержнях, данные реакции
представить в виде продольных сил ![]() ;
;
2) из условия прочности подобрать поперечные сечения стержней;
3) на А4 выполнить чертежи соответствующих поперечных сечений.
Дано:
1) ![]() ;
;
2) ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
3) 1 стержень прямоугольного поперечного сечения, материал Сталь 40 ГОСТ 377-88,
![]() ,
, ![]() ;
;
2 – имеет в
поперечном сечении кольцо, материал латунь ЛЦ40С ГОСТ 17711-93, ![]() ,
, ![]() ;
;
3 –
квадратного поперечного сечения, материал алюминий АК12 ГОСТ 1583-93, ![]() .
.
Решение задачи №1
1. Построение
эпюры продольной силы ![]() . Разбиваем стержень на участки.
Началом и концом участка являются точки приложения внешних сил и опорных
реакций. Для того чтобы не определять опорные реакции из уравнения равновесия,
будем рассматривать отсеченные участки со свободного конца (рисунок 4).
. Разбиваем стержень на участки.
Началом и концом участка являются точки приложения внешних сил и опорных
реакций. Для того чтобы не определять опорные реакции из уравнения равновесия,
будем рассматривать отсеченные участки со свободного конца (рисунок 4).
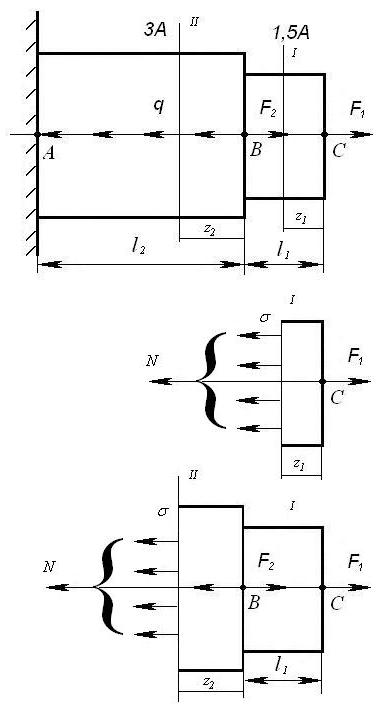
Рисунок 4
Согласно определению, величина продольной силы численно равна алгебраической сумме проекций всех сил, действующих на оставшуюся часть стержня, на ось стержня.
Участок I,
![]()
![]()
Участок II,
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
По полученным
данным строим эпюру ![]() (рисунок 5,а)
предварительно выбрав масштабный коэффициент.
(рисунок 5,а)
предварительно выбрав масштабный коэффициент.
2. Подбор размеров поперечного сечения. Из условия прочности определяем площади и размеры поперечных сечений стержня.
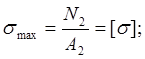
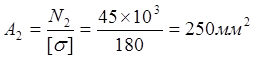 .
.
Площадь и диаметр круглого поперечного сечения определяют по формуле
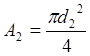 , отсюда
, отсюда
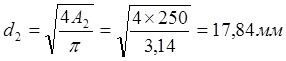 .
.
Площадь поперечного сечения первого участка:
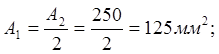
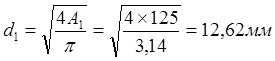 .
.
3. Построение эпюры нормальных напряжений.
Участок I.
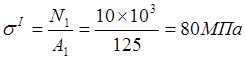 .
.
Участок II.
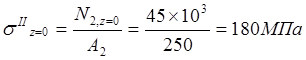 ;
;
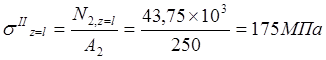 .
.
Стоим эпюру
нормальных напряжений ![]() в масштабе (рисунок 5,б).
в масштабе (рисунок 5,б).
4. Построение эпюры перемещений. Для построения эпюры перемещений используем формулу закона Гука.
При построении
эпюры ![]() учтем, что в точке А (жесткая
заделка) перемещение сечения стержня отсутствует. С этой точки и начинаем
отсчитывать ординаты перемещений.
учтем, что в точке А (жесткая
заделка) перемещение сечения стержня отсутствует. С этой точки и начинаем
отсчитывать ординаты перемещений.
![]()
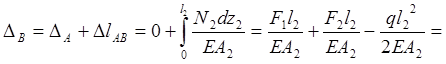
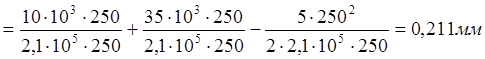 ;
;
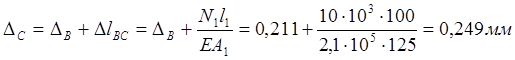 .
.
Строим эпюру перемещений в масштабе (рисунок 5,в).
Проверяем стержень по условию жесткости:
![]() , где
, где ![]() принимаем
конструктивно.
принимаем
конструктивно.
![]() .
.
Вывод: условие жесткости не выполняется.
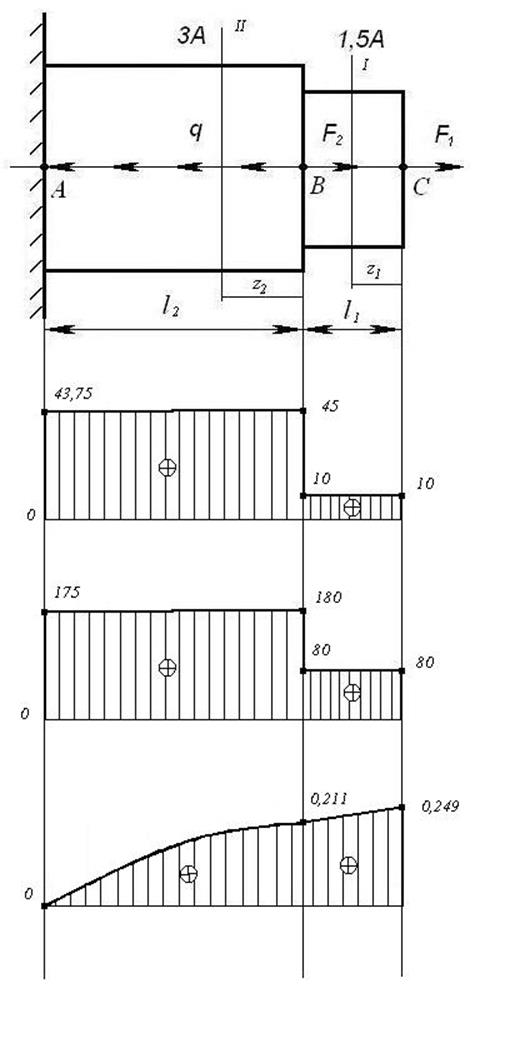
Рисунок 5
Решение задачи №2
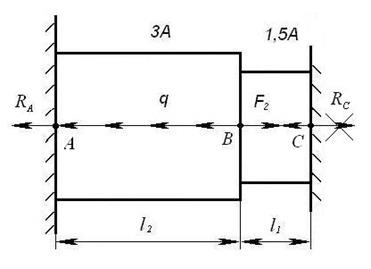
Рисунок 6
1. Нахождение реакций в заделках (рисунок 6). Из условия совместимости деформации определяем реакции в заделках.
![]()
![]()
![]()
![]()
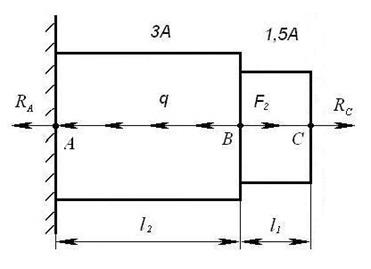
Рисунок 7
Отбрасываем правую заделку
(рисунок 7) и находим реакцию, ![]() .
.
![]()
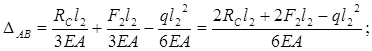
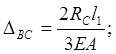
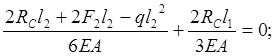
![]()
![]()
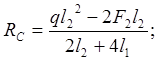
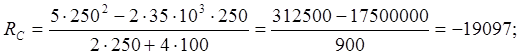
![]()
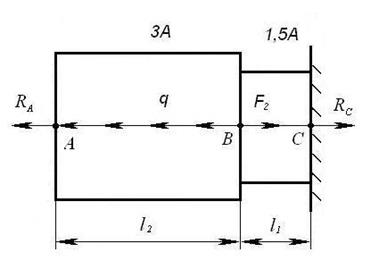 Рисунок 8
Рисунок 8
Отбрасываем
левую заделку (рисунок 8) и находим реакцию,![]() .
.
![]()
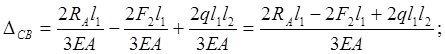
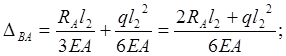
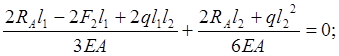
![]()
![]()
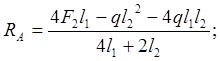
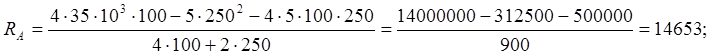
![]()
Выполним проверку,
сложив все силы, действующие на стержень, учтем, что реакция ![]() направлена в противоположную сторону
(рисунок 6).
направлена в противоположную сторону
(рисунок 6).
![]()
![]()
![]()
2. Построение
эпюры продольной силы ![]() . Исходную систему (рисунок 2)
статически неопределимую превращаем в определенную, отбрасывая одну любую из
заделок (рисунок 7). Разбиваем стержень на участки. Началом и концом участка
являются точки приложения внешних сил и опорных реакций. Для того чтобы не
определять опорные реакции из уравнения равновесия, будем рассматривать
отсеченные участки со свободного конца (рисунок 9).
. Исходную систему (рисунок 2)
статически неопределимую превращаем в определенную, отбрасывая одну любую из
заделок (рисунок 7). Разбиваем стержень на участки. Началом и концом участка
являются точки приложения внешних сил и опорных реакций. Для того чтобы не
определять опорные реакции из уравнения равновесия, будем рассматривать
отсеченные участки со свободного конца (рисунок 9).
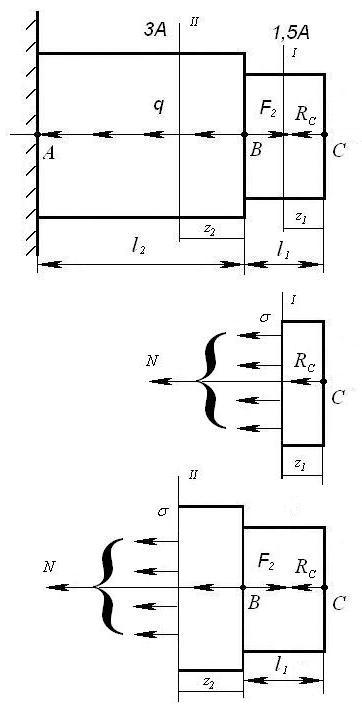 Рисунок 9
Рисунок 9
Согласно определению, величина продольной силы численно равна алгебраической сумме проекций всех сил, действующих на оставшуюся часть стержня, на ось стержня.
Участок I, ![]()
![]()
Участок II, ![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
По полученным
данным строим эпюру ![]() (рисунок 10,а)
предварительно выбрав масштабный коэффициент.
(рисунок 10,а)
предварительно выбрав масштабный коэффициент.
3. Подбор размеров поперечного сечения. Из условия прочности определяем площади и размеры поперечных сечений стержня.
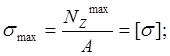
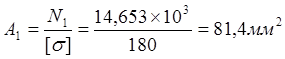 .
.
Площадь и диаметр круглого поперечного сечения определяют по формуле
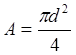 , отсюда
, отсюда
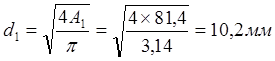 .
.
Площадь поперечного сечения второго участка:
![]()
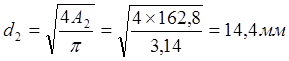 .
.
4. Построение эпюры нормальных напряжений.
Участок I.
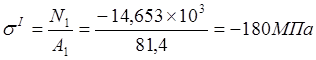 .
.
Участок II.
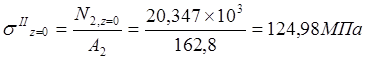 ;
;
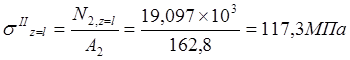 .
.
Стоим эпюру
нормальных напряжений ![]() в масштабе (рисунок 10,б).
в масштабе (рисунок 10,б).
5. Построение эпюры перемещений. Для построения эпюры перемещений используем формулу закона Гука.
При построении
эпюры ![]() учтем, что в точке A (жесткая заделка) перемещение сечения стержня отсутствует. С
этой точки и начинаем отсчитывать ординаты перемещений.
учтем, что в точке A (жесткая заделка) перемещение сечения стержня отсутствует. С
этой точки и начинаем отсчитывать ординаты перемещений.
![]()
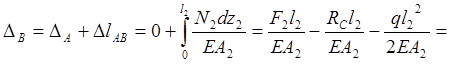
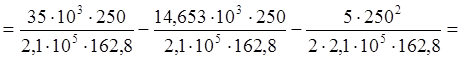
![]()
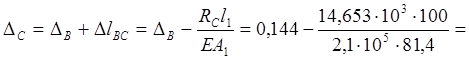
![]() .
.
Строим эпюру перемещений в масштабе (рисунок 10,в).
Проверяем стержень по условию жесткости:
![]() , где
, где ![]() принимаем
конструктивно.
принимаем
конструктивно.
![]() .
.
Вывод: условие жесткости выполняется.
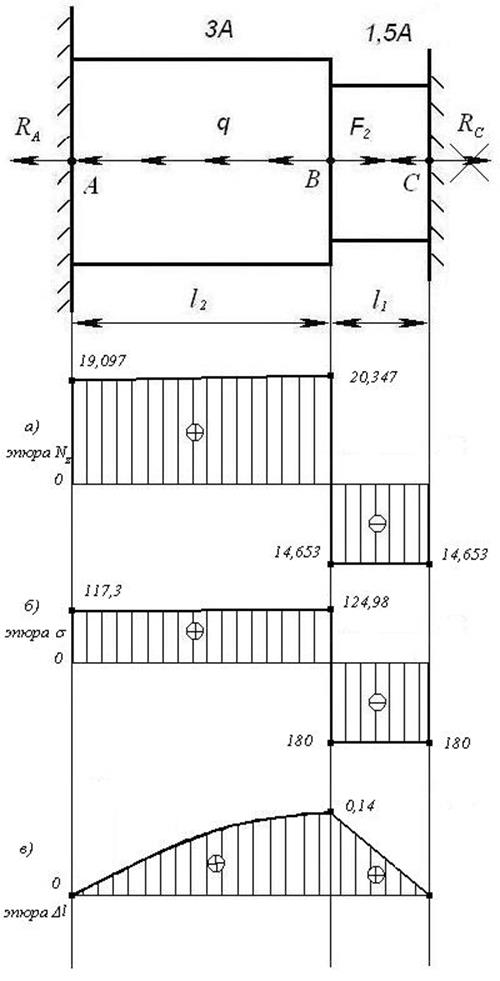
Рисунок 10
Решение задачи №3
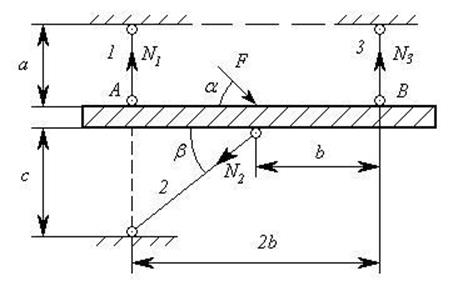
Рисунок 11
1. Сначала
найдем угол ![]() .
.
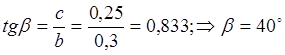
Согласно определению, величина продольной силы численно равна алгебраической сумме проекций всех сил, действующих на ось стержня.
Для того чтобы определить опорные реакции составим уравнения проекции на оси системы координат и уравнения равновесия:
![]()
![]()
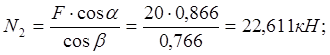
![]()
![]()
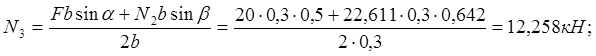
![]()
![]()
![]()
Сделаем
проверку правильности решения, для этого найдем момент всех сил относительно точки
![]() .
.
![]()
![]()
![]() .
.
2. Подбор размеров поперечного сечения. Из условия прочности определяем площади и размеры поперечных сечений стержней.
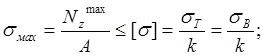
Определим
площадь поперечного сечения для 1 стержня прямоугольного поперечного сечения,
материал Сталь 40, стр.76, таб.20, ГОСТ 377-88, ![]() ,
, ![]() . Рассчитаем допустимое напряжение.
. Рассчитаем допустимое напряжение.
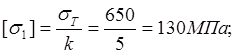
Площадь поперечного сечения для прямоугольника рассчитаем по формуле
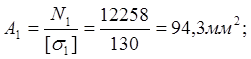
![]()
![]()
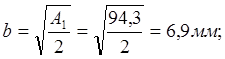
![]()
Определим площадь
поперечного сечения для 2 стержня имеющего в поперечном сечении кольцо,
материал латунь ЛЦ40С, стр.228, таб.85, ГОСТ 17711-93, ![]() ,
,
![]() . Рассчитаем допустимое напряжение.
. Рассчитаем допустимое напряжение.
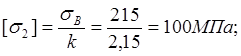
Площадь поперечного сечения для кольца рассчитаем по формуле
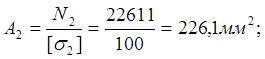
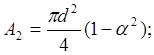
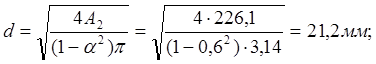
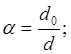
![]()
Определим площадь
поперечного сечения для 3 стержня квадратного поперечного сечения, материал
алюминий АК12, стр.241, таб.98, ГОСТ 1583-93, ![]() .
Рассчитаем допустимое напряжение.
.
Рассчитаем допустимое напряжение.
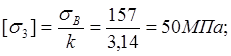
Площадь поперечного сечения для квадрата рассчитаем по формуле
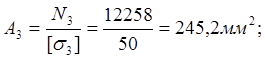
![]()
![]()
![]()
3. Изобразим поперечные сечения на чертежах
Список использованных источников
1. Прикладная механика. Руководство к решению задач:
Учебное пособие/ Е. В. Брюховецкая, Г. А. Кузнецов, Е. Г. Синенко и др. Красноярск:
ИПЦ КГТУ, 2001. 163с.
2. Справочник конструктора-машиностроителя.
Анурьев В. И. 2006, Т1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.