



1.
Группируем первую скобку с четвертой,
вторую с третьей, получим ![]() , заменим
, заменим ![]() , тогда
, тогда ![]() .
Значит
.
Значит ![]() или
или ![]() и
получаем
и
получаем ![]() .
.
Ответ: ![]() .
.
2.
Группируем первую скобку с четвертой,
вторую с третьей, получим ![]() . Заметим, что х=0,
не является корнем уравнения, значит, можно вынести их каждой скобки х и
разделить обе части уравнения на х2. Уравнение примет вид:
. Заметим, что х=0,
не является корнем уравнения, значит, можно вынести их каждой скобки х и
разделить обе части уравнения на х2. Уравнение примет вид: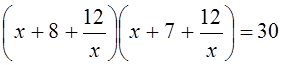 , заменим
, заменим 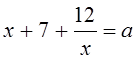 ,
, ![]() . Тогда
. Тогда 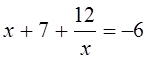 или
или 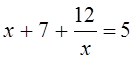 . Умножим каждое из этих уравнений на х,
получим
. Умножим каждое из этих уравнений на х,
получим ![]() , или
, или ![]() , D<0,
решений нет.
, D<0,
решений нет.
Ответ: ![]() .
.
3.
Пусть ![]() , тогда
, тогда
![]() ,
, ![]() ,
, ![]() .
.
Ответ: 144.
4.
Умножим обе части уравнения на ![]() , тогда
, тогда![]() . Пусть
. Пусть
![]() , тогда
, тогда ![]() ,
, ![]() . Тогда
. Тогда ![]() или
или ![]() .
.
Ответ: ![]() .
.
5.
Пусть ![]()
![]() , тогда
, тогда ![]() . Уравнение
примет вид:
. Уравнение
примет вид: ![]() . С учетом, что
. С учетом, что ![]() имеем
имеем ![]() ,
, ![]() .
.
Ответ: ![]() .
.
6.
ОДЗ: ![]() . Пусть
. Пусть ![]() ,тогда
,тогда ![]() . Получаем уравнение
. Получаем уравнение ![]() , возводим обе части уравнения в
четвертую степень:
, возводим обе части уравнения в
четвертую степень: ![]() . Снова замена:
. Снова замена: ![]() тогда
тогда ![]() значит
х2=1, с учетом ОДЗ, х=1.
значит
х2=1, с учетом ОДЗ, х=1.
Ответ: 1.
7.
ОДЗ: ![]() . Приравниваем к нулю
каждый множитель. 1)
. Приравниваем к нулю
каждый множитель. 1)![]()
![]()
![]() . Но
. Но ![]() не
является корнем исходного уравнения, т.к. не подходит по ОДЗ. 2)
не
является корнем исходного уравнения, т.к. не подходит по ОДЗ. 2)![]()
![]() .
.
Ответ: –1, –16, 6.
8.
Возведем обе части уравнения в
квадрат, получим ![]() ,
, ![]() .
Проверка показывает, что х=7, является посторонним корнем.
.
Проверка показывает, что х=7, является посторонним корнем.
Ответ: 10.
9.
При х=2 обе части уравнения
обращаются в ноль, тем не менее, х=2 не является корнем данного
уравнения, т.к. в этом случае ![]() не имеет смысла.
Делим обе части уравнения на
не имеет смысла.
Делим обе части уравнения на ![]() , и возводим обе его
части в квадрат, получим
, и возводим обе его
части в квадрат, получим ![]() .
.
Ответ: 4, –1.
10.
Возводим обе части уравнения в
квадрат: ![]() ,
,![]()
![]()
![]()
![]() . Проверка
показывает, что х= –3 посторонний корень.
. Проверка
показывает, что х= –3 посторонний корень.
Ответ:–2.
11.
![]() ,
тогда
,
тогда 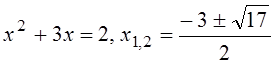 или
или ![]() ,
, ![]() .
.
Ответ: 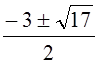 , –2, –1.
, –2, –1.
12.
![]() или
или ![]() .
.
Ответ:2, 4, ![]() .
.
13.
Первое уравнение является однородным,
т.к. каждое его слагаемое имеет одинаковую степень 2. Делим обе части этого
уравнения на ![]() . Получим:
. Получим: 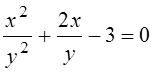 .
Заменим
.
Заменим 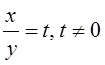 , получим
, получим ![]() , тогда
, тогда
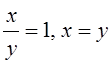 или
или 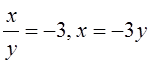 .
Подставим найденные соотношения во второе уравнение исходной системы. При х=у,
получим
.
Подставим найденные соотношения во второе уравнение исходной системы. При х=у,
получим ![]() . При х = –3у:
. При х = –3у: ![]() , нет решений.
, нет решений.
Ответ: ![]() .
.
14. Решаем неравенство методом интервалов. Числитель обращается в ноль при х1,2=0 и х3= –3. Знаменатель обращается в ноль при х1= –1 и х2=6.
 Ответ:
Ответ:![]() .
.
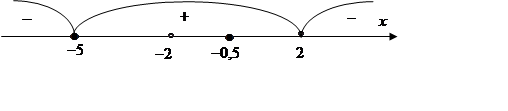 15. Решаем неравенство методом интервалов. Числитель обращается
в ноль при х1,2= –0,5 и х3= –5. Знаменатель
обращается в ноль при х1,2= ±2 и х3=
–2. Ответ:
15. Решаем неравенство методом интервалов. Числитель обращается
в ноль при х1,2= –0,5 и х3= –5. Знаменатель
обращается в ноль при х1,2= ±2 и х3=
–2. Ответ:![]() .
.
16.
Неравенство равносильно системе
неравенств: 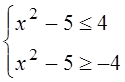 ,
, 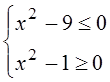 ,
, 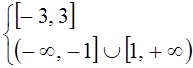 , общее решение:
, общее решение: ![]() .
.
Ответ: ![]() .
.
17. Неравенство равносильно совокупности неравенств: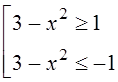 ,
, 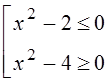 ,
, 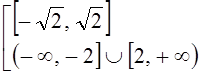 . Общее решение:
. Общее решение: ![]() .
.
Ответ: ![]() .
.
18.
Уравнение имеет два различных
действительных корня, если 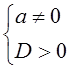 , запишем эти условия
для данного уравнения:
, запишем эти условия
для данного уравнения: 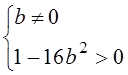 ,
, 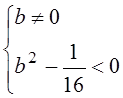 ,
, 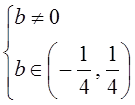 .
Общее решение:
.
Общее решение: 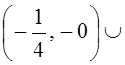
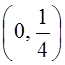 .
.
Ответ: 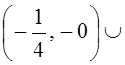
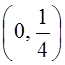 .
.
19.
График данной квадратичной функции
лежит ниже оси Ох при любых значениях х. если D<0, т.е. 36–32с < 0, 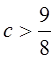 .
.
Ответ:2.
20.
Уравнение имеет два различных действительных
корня разных знаков, если 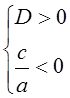 , запишем эти условия
для данного уравнения:
, запишем эти условия
для данного уравнения: 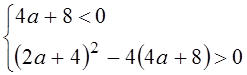 ,
, 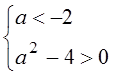 ,
, 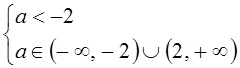 .
.
Ответ: ![]() .
.
21.
Данное уравнение равносильно системе:
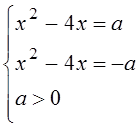 , следовательно, каждое из уравнений
системы должно иметь два различных корня (D> 0).
, следовательно, каждое из уравнений
системы должно иметь два различных корня (D> 0).
1)
![]() . 2)
. 2) ![]() .
Учитывая, что а>0, получаем 0<a<4.
.
Учитывая, что а>0, получаем 0<a<4.
Ответ: ![]() .
.
22.
ОДЗ: ![]() .
Приравниваем к нулю каждый множитель в левой части данного уравнения, получим:
.
Приравниваем к нулю каждый множитель в левой части данного уравнения, получим: ![]() и
и ![]() .
Исходное уравнение имеет один корень, если
.
Исходное уравнение имеет один корень, если ![]() , то
есть при
, то
есть при ![]() , или, если
, или, если ![]() не
подходит по ОДЗ, то есть
не
подходит по ОДЗ, то есть ![]() . Общее решение
. Общее решение![]() .
.
Ответ: ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.