Плоскости и их общие точки. Вычисление площади правильного треугольника

Контрольная работа по математике №5, 11 класс

Решения заданий части А

А1. Для того, чтобы плоскости совпадали, необходимо, чтобы они имели две общие точки. Утверждение не является достаточным, так как и пересекающиеся плоскости имеют две общие точки.                                          Ответ №1.

А2. Для того чтобы прямая лежала в плоскости, необходимо, чтобы она имела с плоскостью одну общую точку. Прямая, пересекающая плоскость тоже имеет с ней одну общую точку, следовательно, утверждение не является достаточным.                                                                                                    Ответ №1.

А3. Боковое ребро наклонного параллелепипеда может быть перпендикулярно  одной стороне основания. Если боковое ребро наклонного параллелепипеда перпендикулярно  двум сторонам основания, тогда оно будет перпендикулярно плоскости основания, следовательно,  параллелепипед  уже не наклонный, а прямой.                                                                                           Ответ №1.

А4. Если две плоскости перпендикулярны, то прямая перпендикулярная линии пересечения перпендикулярна любой прямой, лежащей в другой плоскости.  Прямая параллельная линии пересечения, будет параллельна другой плоскости (значит и утверждение №1 тоже неверно).                                      Ответ №2.

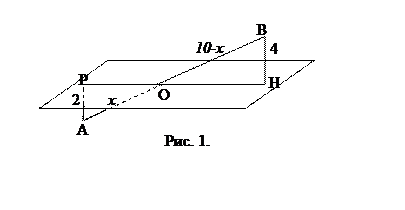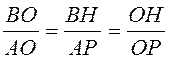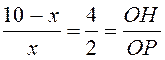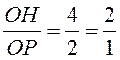
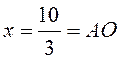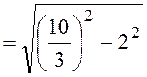
А5. Проекцией отрезка АВ на плоскость является отрезок РН (Рис. 1). . Прямоугольные треугольники ВОН и РОА подобны (по двум углам), значит, . Обозначим , . Тогда . Следовательно,    и     .  Теперь находим ОР по теореме Пифагора из : 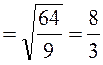, значит, 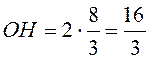. В итоге 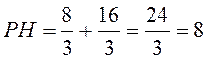.                                        Ответ №4.

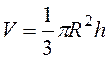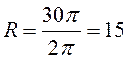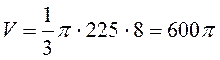А6. . . По условию задачи   , по теореме Пифагора из  . В итоге .                                    Ответ №3.

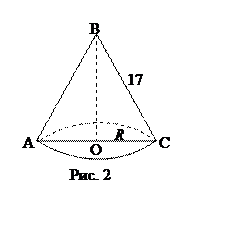
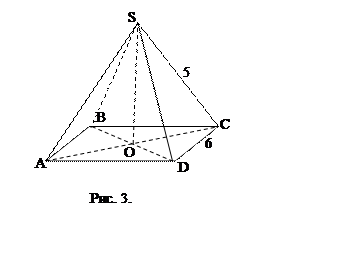А7. Искомое расстояние – высота SO пирамиды SABCD (рис. 3.) По теореме Пифагора из  , SC – боковое ребро пирамиды, 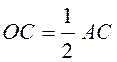. По теореме Пифагора из  . Значит, . Тогда, .                   Ответ №3.

А8. Площадь поверхности правильного тетраэдра состоит из четырех правильных треугольников. Площадь правильного треугольника вычисляется по формуле: 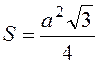. Значит, для тетраэдра: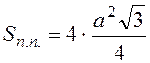 . По условию задачи , тогда .                                             Ответ №1.

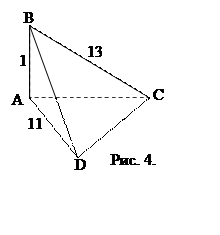
А9. По теореме Пифагора из  (рис. 4) (по условию ). Аналогично, из :  (по условию ) Следовательно,   .               Ответ №1.

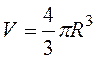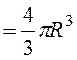
А10. Площадь поверхности шара вычисляется по формуле: , объем шара . По условию .                                                                      Ответ №3.