


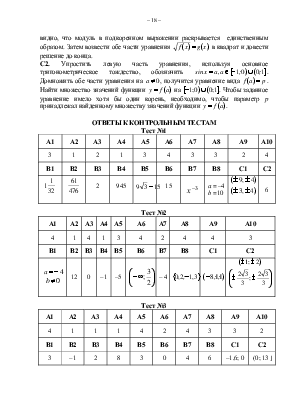

В8. Указать число корней
уравнения ![]()
на промежутке ![]()
Часть III
(Записать полное решение)
С1. Решить уравнение ![]()
С2. Найти все значения р,
при которых уравнение ![]() имеет хотя бы один корень.
имеет хотя бы один корень.
A1. Преобразовать корни к подобным и выполнить действия.
A2. Найти НОК и НОД данных чисел и поделить.
A3. Процент от числа находим умножением этого числа на заданный процент.
A4. Использовать формулы суммы и общего члена арифметической прогрессии.
A5.
Использовать формулу ![]() , где P
– делимое, D – делитель, Q
– частное, R – остаток.
, где P
– делимое, D – делитель, Q
– частное, R – остаток.
A6. Использовать свойства корней.
A7. Выполнить сокращение дробей.
A8. Применить свойство умножения степеней с одинаковым основанием.
A9. Преобразовать корни к подобным и выполнить действия.
A10. Использовать свойства корней.
B1. Записать пропорцию, выразить четвёртый член через остальные, затем через первый.
B2.
Применить формулу 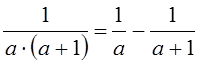 .
.
B3. Выделить целую часть делением числителя на знаменатель и ответить на вопрос задачи.
B4. Записать ряд чисел, удовлетворяющий условию задачи и применить формулы суммы и общего члена арифметической прогрессии.
B5. Выделить полный квадрат в числителе дроби и освободиться от иррациональности в знаменателе.
B6. Применить свойства степени с действительным показателем.
B7. Применить формулы разности квадратов и суммы кубов.
B8. Использовать определение равенства двух многочленов.
C1. Разложить левую часть уравнения на множители.
C2. Сумму корней обозначить через y и возвести в квадрат обе части получившегося равенства.
Тест №2
A1. Найти x и y из второго и третьего уравнений и подставить в первое.
A2.
Сделать замену 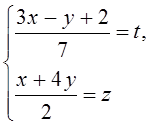 .
.
A3. Решить уравнение, учитывая область определения уравнения и ограничения по знаку.
A4.
Выразить x из системы уравнений и решить
неравенство, так как ![]() .
.
A5. Рассмотреть графическое решение.
A6.
Составить систему неравенств 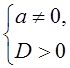 .
.
A7. Использовать теорему Виета.
A8.
Заметить, что ![]() является корнем уравнения, после
чего поделить обе части уравнения на
является корнем уравнения, после
чего поделить обе части уравнения на ![]() и решить его.
и решить его.
A9.
Решить систему неравенств 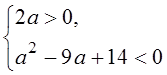 .
.
A10.
Учитывая знак x, раскрыть модуль ![]() и решить два уравнения.
и решить два уравнения.
B1. Отношения коэффициентов при неизвестных должны быть равными, но не равны отношению свободных членов.
B2. Раскрыть модуль и сделать отбор значений.
B3.
Привести уравнение к виду ![]() и решить систему
и решить систему 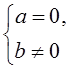 .
.
B4. Отношения коэффициентов при неизвестных и свободных членов должны быть равными.
B5. Разложить на множители числитель дроби и сократить, затем решать уравнение.
B6.
Решить систему неравенств 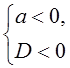 .
.
B7. Использовать теорему Виета.
B8.
Сделать замену ![]() .
.
C1.
Ввести переменную t: 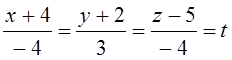 .Выразить
x, y, z через t.
.Выразить
x, y, z через t.
C2.
Обе части второго уравнения системы умножить на ![]() ;
сложить уравнения; решить однородное уравнение.
;
сложить уравнения; решить однородное уравнение.
А1. Решить методом интервалов.
А2. Возвести обе части уравнения в квадрат, решить полученное уравнение и сделать проверку.
А3. Найти ОДЗ. Перенести один корень в правую часть неравенства, возвести обе части в квадрат и решить полученное неравенство. Ответ записать с учетом ОДЗ.
А4. Возвести обе части уравнения в квадрат. Ответ записать с учетом ОДЗ.
А5. Аналогично заданию А3.
А6. Упростить, используя основное тригонометрическое тождество.
А7. Упростить, используя основное тригонометрическое тождество, решить полученное уравнение с учетом ОДЗ.
А8. Множество значений
функции ![]() умножить на два и вычесть единицу (см.
заданную функцию).
умножить на два и вычесть единицу (см.
заданную функцию).
А9. Расписать правую часть уравнения по формуле двойного угла, перенести все в левую часть и вынести за скобку общий множитель.
А10. Упростить, используя тригонометрические формулы сложения и приведения.
В1. Выразить y в каждом из уравнений системы и решить графически.
В2. Подставить в заданное
неравенство ![]() , решить относительно а и ответить
на вопрос задачи.
, решить относительно а и ответить
на вопрос задачи.
В3. Первый способ. Выделить полный квадрат под каждым из корней, извлечь арифметический квадратный корень из полного квадрата, учитывая заданные значения х. Второй способ. Обозначить искомое выражение через y, возвести обе части полученного равенства в квадрат, упростить и вычислить значение y. При выборе ответа учитывать, что y>0 (по определению арифметического квадратного корня).
В4. Перенести все в правую часть, привести к общему знаменателю и решить методом интервалов.
В5. Приравнять к нулю каждый из множителей, количество корней ограничить ОДЗ.
В6. Упростить, используя формулы приведения и формулу двойного угла, затем вынести в числителе за скобку общий множитель.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.