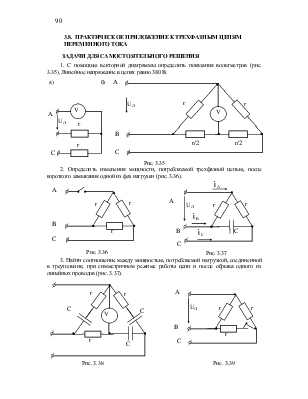













1. С помощью векторной диаграммы определить показания вольтметров (рис. 3.35). Линейное напряжение в цепях равно 380 В.


2. Определить изменения мощности, потребляемой трехфазной цепью, после короткого
замыкания одной из фаз нагрузки (рис. 3.36).

3. Найти соотношение между мощностью,
потребляемой нагрузкой, соединенной в треугольник, при симметричном режиме
работы цепи и после обрыва одного из линейных проводов (рис. 3.37).
4. Используя векторную диаграмму, определить линейные токи цепи (рис. 3.38), если UЛ = 380 В; r = 1/wC = 380 Ом.
5. Определить линейные токи в цепи (рис 3.39) при замкнутом и разомкнутом ключе, если UЛ = 380 В; r = 190 Ом.
6. Какое напряжение зарегистрирует вольтметр в цепи (рис. 3.38), если линейное напряжение источника UЛ = 380 В; r = 1/wC?
7. Дано: Uл = 380 В![]() ; xc = 50 Ом;
r = 50 Ом; xL = 300 Ом.
; xc = 50 Ом;
r = 50 Ом; xL = 300 Ом.
Рассчитать токи в треугольнике и линии (рис. 3.40).
 |
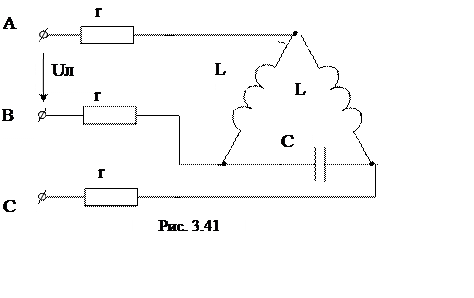
8. Дано: Uл = 220 В; r = 30 Ом; wL = 30 Ом; 1/wc = 30 Ом.
Найти токи в нагрузке и линии (рис. 3.41).
 |
9. Дано: E = 220 В; rл = 10 Ом; хл = 10 Ом; r = 30 Ом; хс = 40 Ом; хL = 50 Ом.
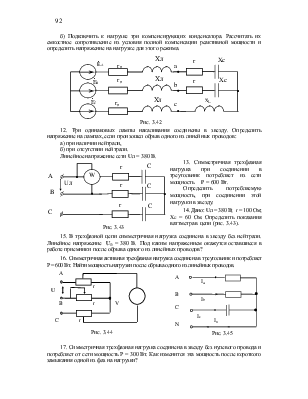
Трехфазный генератор питает через линию, обладающую активно-индуктивным сопротивлением, нагрузку, соединенную в звезду (рис. 3.42).
Требуется определить напряжения на фазах нагрузки?
10. Через трехпроводную линию с сопротивлением ZЛ = 100 Ом, питается симметричная трехфазная нагрузка, соединенная треугольником. Сопротивление фазы нагрузки Zн = j300 Ом. Найти напряжения на фазах нагрузки, если линейное напряжение на входе линии равно 220 В.
11. Симметричная трехфазная нагрузка соединена в звезду и питается через трехпроводную линию от источника UЛ = 380 В. Сопротивление линии ZЛ = j20 Ом. Сопротивление фазы нагрузки: ZН = 100 + j60 Ом.
а) Определить напряжение на фазе нагрузки.
 |
12. Три одинаковых лампы накаливания соединены в звезду. Определить напряжение на лампах, если произошел обрыв одного из линейных проводов:
а) при наличии нейтрали, б) при отсутствии нейтрали.
Линейное напряжение сети Uл = 380 В.
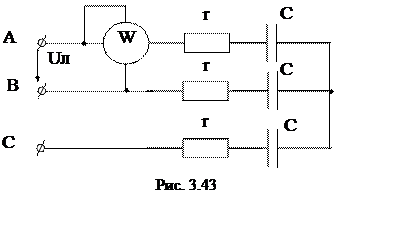 13.
Симметричная трехфазная нагрузка при соединении в треугольник потребляет из
сети мощность P = 600 Вт.
13.
Симметричная трехфазная нагрузка при соединении в треугольник потребляет из
сети мощность P = 600 Вт.
Определить потребляемую мощность, при соединении этой нагрузки в звезду.
14. Дано: Uл = 380 В; r = 100 Ом; Xc = 60 Ом. Определить показания ваттметра в цепи (рис. 3.43).
15. В трехфазной цепи симметричная нагрузка соединена в звезду без нейтрали. Линейное напряжение UЛ = 380 В. Под каким напряжением окажутся оставшиеся в работе приемники после обрыва одного из линейных проводов?
16. Симметричная активная трехфазная нагрузка соединена в треугольник и потребляет Р = 600 Вт. Найти мощность нагрузки после обрыва одного из линейных проводов.
17. Симметричная трехфазная нагрузка соединена в звезду без нулевого провода и потребляет от сети мощность Р = 300 Вт. Как изменится эта мощность после короткого замыкания одной из фаз на нагрузки?
18. Три одинаковых сопротивления при соединении в треугольник потребляют от трехфазной сети мощность Р = 600 Вт.
Чему будет равна потребляемая мощность, если сопротивления соединить в звезду?
19. Определить ток трехфазного электродвигателя, обмотки которого соединены в звезду, если известно, что РН = 1,2 кВт; U = 380 В; h = 0,9; cosj = 0,8.
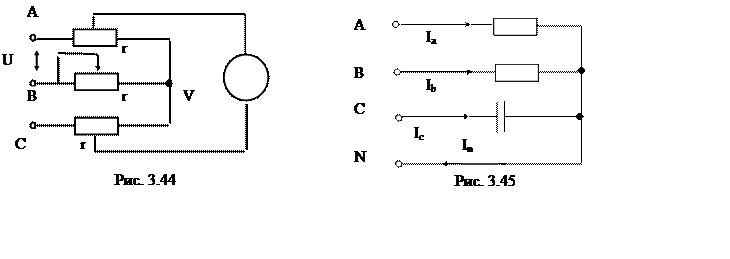
20. Как будут изменяться показания вольтметра (рис. 3.44) при изменении сопротивления в фазе В от r до 0? (U = 380 В).
21. Найти ток в нейтрали (рис. 3.45), если известно, что токи в фазах равны 1 А.
1.* В цепи (рис 3.46, а) фазное напряжение источника: Uф = 220 В, сопротивление нагрузки: r = 220 Ом; xc = 220 Ом.
Требуется определить показания амперметра.
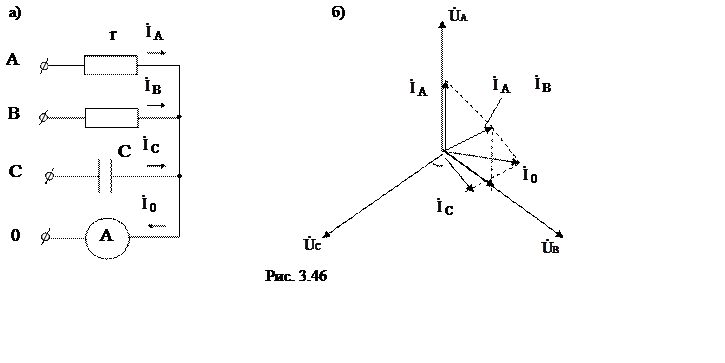
Решение:
Данную задачу проще всего решить с помощью векторной диаграммы (рис 3.46, б).
По модулю токи всех фаз нагрузки равны 1 А (Iф = Uф/Zф; Iф = 220/220 = 1A).
При этом токи фаз A и B
совпадают по фазе с соответствующими напряжениями, а ток фазы C
опережает напряжение U0 на ![]() /2.
/2.
Амперметр включен в нейтральный провод, ток которого равен сумме фазных токов нагрузки:
![]() 0 =
0 = ![]() A +
A +
![]() B +
B +
![]() C.
C.
Эту сумму несложно найти из векторной диаграммы.
Причем сумма ![]() A +
A + ![]() B равна по модулю 1 А, а угол между полученным вектором
и вектором
B равна по модулю 1 А, а угол между полученным вектором
и вектором ![]() C оказывается
равным 90
C оказывается
равным 90![]() .
Вследствие этого
.
Вследствие этого ![]() 0
=
0
= ![]() А. Таким образом, амперметр покажет 1,41 А.
А. Таким образом, амперметр покажет 1,41 А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.