Трехфазные цепи переменного тока: Задачи для самостоятельного решения, страница 2

2.^* Дано: r = 100 Ом;  x_L = 100 Ом;  x_c = 100 Ом;  U_Л = 380 В.

Определить напряжения и токи в фазах при замкнутом и разомкнутом ключе (рис. 3.47).

Решение:

При замкнутом ключе напряжения на фазах нагрузки равны фазным напряжениям источника:

U_ф = U_Л/ = 380/ = 220 В;

_А = 220 В; _B = 220e^-j120 В;

U_c = 220e^j120 В.

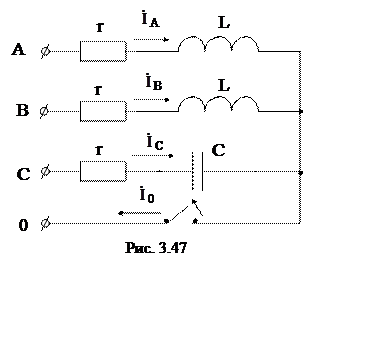Токи в фазах нагрузки:

=_А/Z_A;

 = 220/(100 + j100) = 220/100e^j45 = = 1.556e ^-j45A;

_B = _B/Z_B ;

_B = 220e ^-j120/(100 + j100) = 1,556e ^-j165A;

_C = _C/Z_C;

_C =220e ^j120/(100 – j100) = 1,556e ^j165A.

Ток в нейтрали:

₀ = _A + _B + _C;

₀ =1,1 – j1,1 – 1,503 – j0Ю4027 – 1,503 + + j0,4027 = 1,906 – j1,1 = 2,2e ^j150A.

При отсутствии нейтрального провода (ключ разомкнут) цепь можно рассчитать методом двух узлов.

Напряжение смещения нейтрали:

 = =  =

= ;

 =  =  =  =

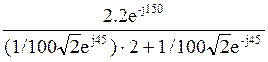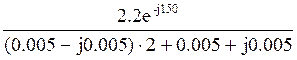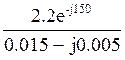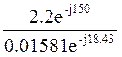= 139,1e^-j131.57 = -92,3 – j104,1 В.

Напряжения на фазах нагрузки:

= _{А – 0} = 220 + 92.3 + j104.1 =;

 = 329.3e^j18.43 B.

 = _{B – 0} =;

 = -110 – j190.5 + 92.3 +j104.1 =

= -17.7 – j86.4 = 88.19e^-j101.58 B.

= _{C – 0} =;

= -110 + j190.5 + 92.3 + j104.1;

= -17.7 + j294.6 = 295.1e^j93.44 B.

Токи  в фазах нагрузки:

_A = /Z_A;

_A = 329.3e^j18.43/100e^j45 = 2.329e ^-j36.57 A.

_B = /Z_B;

 _B = 88.19e^-j101.58/100e^j45 = 0.624e^-j146.58 A.

_CA = /Z_C;

_CA = 295.1e ^j93.44/100e^-j45=2.087e ^j138.44A.

На рис. 3.48 приведена векторная топографическая диаграмма напряжений, совмещенная с векторной диаграммой токов для трехфазной цепи при отсутствии нейтрального провода.

3. К трехфазному симметричному генератору синусоидального напряжения подсоединены через воздушную линию симметричная динамическая  и несимметричная статическая нагрузка (рис. 3.49). Такой вид несимметрии носит название поперечной.

Для анализа этой цепи рассмотрим три электрических схемы несимметричной нагрузки, которые представлены на рис. 3.50. Анализ будем проводить при следующих параметрах:

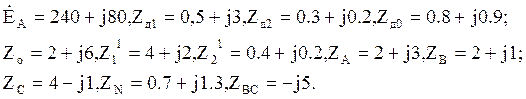
Здесь  – сопротивление обмоток генератора прямой, обратной  и нулевой последовательностей;  – сопротивление динамической нагрузки прямой и обратной последовательностей;  – сопротивление нейтрального провода;  – сопротивление воздушной линии передачи (сопротивление линии с током различных последовательностей примем одинаковыми).

Для расчета несимметричных режимов в такой цепи применяется метод симметричных составляющих.

Заменим несимметричную нагрузку тремя источниками ЭДС с неизвестными напряжениями ,  системой, которая, помимо генератора с симметричной системой ЭДС, содержит источники с несимметричными напряжениями.

Разложим эти напряжения на симметричные составляющие и в результате  получим симметричную схему (рис. 3.51)

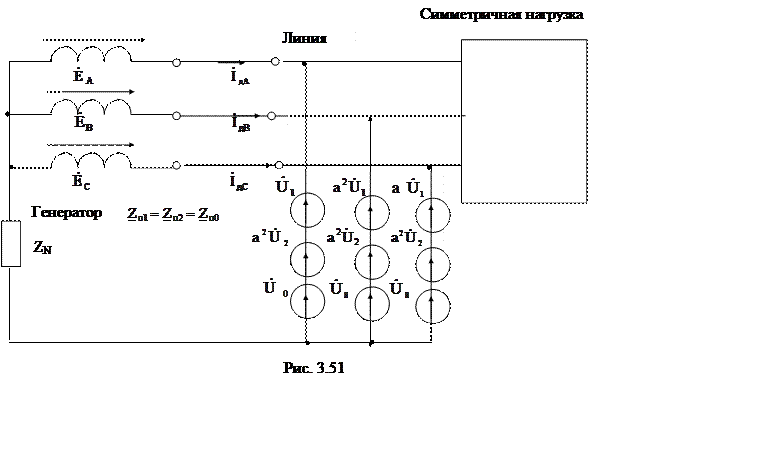
Приняв фазу А за основную построим для различных последовательностей три независимых схемы, показанные на рис. 3.52, 3.53 и 3.54.

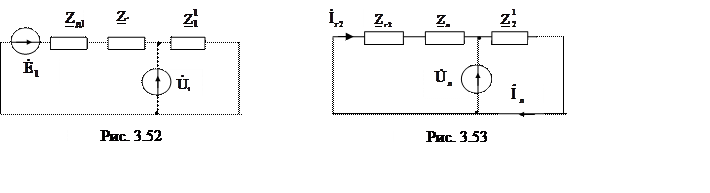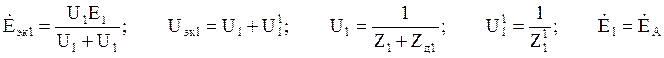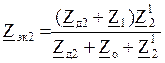Преобразуем эти схемы к простейшему виду, не затрагивая при этом ветвей с источниками неизвестных напряжений . Так, схема прямой последовательности (рис. 3.18) преобразуется в схему (рис. 3.21), а схема (рис 3.19) – в схему (рис. 3.22), где:

;

;    ;     ,

где    .

Схема нулевой  последовательности в преобразовании не нуждается.

Для каждой из трех схем напишем уравнения по второму закону Кирхгофа.

В этих уравнениях шесть неизвестных:

Дополнительные три уравнения составляются на основании заданной схемы и параметров несимметричного приемника.

Составим эти уравнения для всех трех схем статической нагрузки.

Для первой нагрузки (рис. 3.50, а):    

;

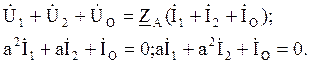
Для второй нагрузки (рис. 3.50, б):

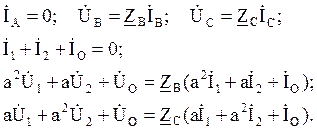
Для третьей нагрузки (рис. 3.50, в):

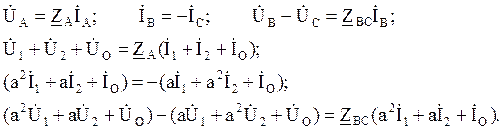
Объединим каждую из последних трех систем с основной системой уравнений.  При этом получим три системы уравнений:

первая система вторая система

третья система

Подставим в эти системы уравнений численные значения коэффициентов:

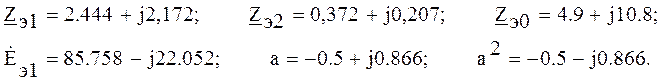
Решим эти системы. В результате чего  получим для первой системы:

Для второй системы уравнений:

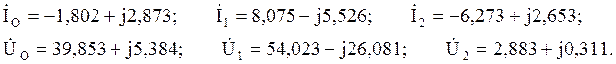
Для третьей системы уравнений:

      

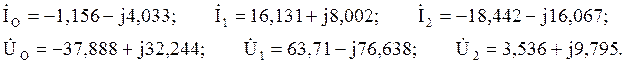
Используя симметричные составляющие, определим фазные токи и напряжения в генераторе динамической и симметричной нагрузках для соответствующих схем.

Для схемы (рис. 3.50, а)

а) Токи и напряжения в несимметричной нагрузке:

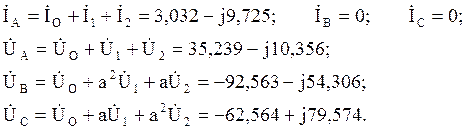
б) Токи в динамической нагрузке

Вначале, используя схему соответствующей последовательности, найдем симметричные составляющие токов:

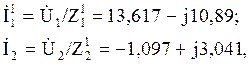
а затем фазные токи:

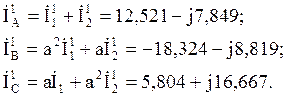
В качестве проверки можно использовать для данной нагрузки первый закон Кирхгофа: , (так как в этой нагрузке отсутствует нейтральный провод).

в) Токи в фазах генератора

Вначале также определяются симметричные составляющие токов, причем они могут быть определены из первого закона Кирхгофа или  из второго , так как симметричные составляющие напряжений на несимметричной нагрузке известны: