Высказывания. Операции дизъюнкции, конъюнкции и отрицания. Пропозициональные формулы, булевы функции и их количество. Класс монотонных функций. Полнота систем булевых функций, страница 9

1. Если т — 1, то это ребро является петлей, которая и будет эйлеровой цепью.

2.  Пусть существует эйлерова цепь для связных графов с четными вершинами и с числом ребер меньшим т.

3.  Рассмотрим связный граф G c m ребрами, имеющий только четные вершины. Стартуем из любой вершины х и будем идти по ребрам, удаляя пройденные ребра. Поскольку все вершины графа были четными, то мы в конце концов вернемся в вершину х. Граф G', который остался непройденным после этого, может иметь несколько компонент связности, но каждая такая компонента содержит только четные вершины и, следовательно, имеет эйлерову цепь. Далее пройдем по первоначальному маршруту еще раз, добавляя по пути эйлеровы цепи компонент связности графа G' и получим эйлерову цепь всего графа G. Теорема доказана.

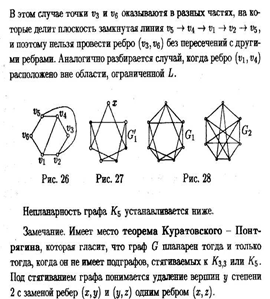
§ 6. Теорема Эйлера о плоских графах

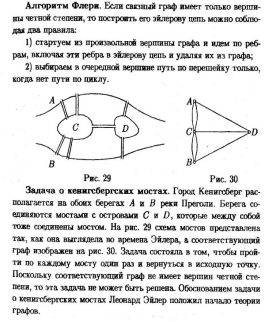
§ 9. Деревья. Цикломатическое число графа

Определение 1. Связный граф называется деревом, если он не имеет циклов. Граф называется лесом, если каждая его компонента связности является деревом.

Свойство 1. Если Г — дерево, то т = п — 1, где т — количество его ребер, a n — число его вершин.

Доказательство проведем индукцией по числу ребер т.

1.  Если m = 0, то n = 1 и формула т = n— 1 верна.

2.   Пусть эта формула верна для деревьев с количеством ребер меньшим, чем т.

3.  Рассмотрим дерево Т с т ребрами и удалим из него ребро g. Поскольку g - перешеек, то получатся два дерева Т₁ и T₂, для которых выполнены равенства m₁ = п₁ — 1 и m₂ = n₂— 1. Учитывая, что m₁ + т₂ = m - 1 и n₁ + n₂ = n, мы получим искомое равенство m = n — 1 для дерева T.

Следствие. Если Т — лес из kдеревьев, то т = п —  k.

Свойство 2. Любые две вершины дерева можно соединить розно одной элементарной цепью.

Свойство 3. Если к ребрам дерева добавить еще одно ребро (без добавления новых вершин), то появится цикл, т.к. нарушится равенство m = n — 1.

Часто в дереве выделяют одну из вершин, которую называют корнем дерева и все ребра ориентируют в направлении от этого корня, такое ориентированное дерево называется корневым.

§ 11. Хроматический многочлен

Определение 1. Хроматическим многочленов графа Gназывается количество способов раскраски Gс помощью х красок, обозначаемое П(G, x).

§ 10. Хроматическое число графа

Определение 1. Говорят, что граф раскрашивается k красками, если каждой вершине графа можно приписать одну из к красок так, чтобы смежные вершины были раскрашены в разные цвета.

Замечание. Граф с петлями раскрасить нельзя, т.к. в нем имеется вершина, смежная самой себе. Наличие кратных ребер очевидно не влияет на раскрашиваемость графа. Учитывая эти два обстоятельства, мы будем рассматривать в этом параграфе только простые графы.

Определение 2. Хроматическим числом графа Gназывается наименьшее число красок, которыми его можно раскрасить. Это число обозначается через x(G)

Свойство 1. Если Т — дерево, имеющее более одной вершины, то х(Т) = 2.

Доказательство. Зафиксируем некоторую вершину x₀ данного дерева Т и разобьем множество всех его вершин на два подмножества Ко и К₁. Во множество К ₀ отнесем все вершины, которые соединяются с x₀элементарной цепью четной длины, а К₁ будет множеством всех вершин, которые соединяются с x₀элементарными цепями нечетной длины. Легко видеть, что смежные вершины попадают в разные классы и поэтому можно раскрасить вершины из Ко одним цветом, а из К₁ - другим.

Свойство 2. еcли x(G₁) = р, х(G₂) = q, то x(G₁ + G₂) =P+q-

Доказательство основано на том, что при соединении двух графов G₁ и G₂  каждая вершина графа G₁становится смежной с каждой вершиной графа G₂, поэтому краски графа G₁нельзя использовать для раскрашивания графа G₁

§ 12. Обход графа в глубину и в ширину