Определение 1. Контактом (переключателем, двухполюсником) называется устройство, которое может иметь два состояния: О и 1. Если к имеющимся у устройства двум полюсам подать напряжение, то в состоянии 1 возникает ток, а в состоянии 0 устройство ток не пропускает. Физически контакты можно реализовать с помощью реле или соответствующих транзисторных схем
Из контактов, соединяя их в полюсах, можно собрать контактную схему, в которой выделяются два полюса, и подается на них напряжение.
В зависимости от состояний контактов схема либо пропускает ток (состояние 1), либо не пропускает (состояние 0). еcли состояния контактов принадлежат
§ 10. Классы функций, сохраняющих 0 или 1
Определение 1. Булева функция f сохраняет константу 0. если f(0,0,... ,0) = 0. Класс всех БФ, сохраняющих 0, обозначается через Ко. Функция f сохраняет 1, если f(1,1,... , 1) = 1. класс таких функций обозначается через К1.
Теорема о замкнутости классов K0 и К1. Каждый из классов K0 и К1 замкнут относительно суперпозиции, т.е. суперпозиция функций, принадлежащих одному из этих классов, снова принадлежит тому же классу.
Доказательство. Пусть функции f(t1,.. , tn) и gi{xi,... ,хm), где i — 1,2,... ,n принадлежат классу Ко. Тогда их суперпозицияh(x1... ,xm) = f(g1(x1,... ,xm),... ,gn(x1,... ,xm)) принадлежит Ко, т.к. h(0,... ,0) = f(g1(0,... ,0),... ,gn(0,... ,0)) = = f(0,... ,0) =0 Замкнутость К1 доказывается аналогично.
§ 13. Класс линейных булевых функций
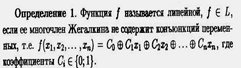
, то состояние схемы является булевой
функцией у = f(x1,... , хп),
которая называется функцией проводимости схемы.
Свойство 1. Если схема состоит из контактов х1 и х2, соединенных последовательно (см. рис. 1), то она имеет функцию проводимости у = x1 ■ Х2; если же схему составить из контактов xi и x2, соединенных между собой параллельно (см. рис. 2), то ее функцией проводимости будет у = x1 V Х2
Теорема о контактной схеме. По любой булевой функции f можно построить контактную схему, для которой f является функцией проводимости.
Доказательство. Еcли f{x1 х2, ...,xп) = 0, то ей соответствует схема, не имеющая контактов. Если же f{x1 х2, ...,xп)<>0, то ее можно реализовать в ДНФ. Каждую элементарную конъюнкцию, из которых состоит ДНФ, реализуем последовательной цепочкой контактов, между собой эти цепочки соединим параллельно. Полученная схема имеет f своей функцией проводимости. Теорема доказана.
Одну и ту же функцию проводимости могут иметь несколько контактных схем. Для построения схемы с возможно меньшим числом контактов обычно используют минимальную ДНФ.
§ 11. Класс самодвойственных функций
Определение
1. Булева функция f называется самодвойственной, если 
Класс самодвойственных функций обозначается через S.
Из определения 1 следует, что самодвойственная функция на противоположных наборах аргументов принимает противоположные значения
Теорема о замкнутости класса S. Класс самодвойственных функций замкнут относительно суперпозиции.
Доказательство проведем на языке функциональных схем. Рассмотрим функциональную схему, составленную из самодвойственных элементов. Если значения сигналов на входах этой схемы поменять на противоположные, то сигналы на выходах всех ее элементов тоже поменяются на противоположные, поскольку они самодвойственных. Значит и сигнал на выходе схемы тоже поменяется, т. к. он является выходом одного из элементов схемы.
Лемма о несамодвойственной функции. Суперпозицией несамодвойственной функции f(x1, x2,... , хп) и отрицания х можно получить константу.
Доказательство. Поскольку f <> S, то можно указать такие противоположные строчки в таблице истинности, на которых эта функция принимает одинаковые значения. Пусть f(--a1,... ,--ап) = = f(a1,... ,an,). Рассмотрим функцию g(х) = f(xa1,...xan), которая получена суперпозицией f и отрицание х, поскольку х° = --х. Имеем: g(0) = f(0а1,0a2,... ,0аn) = f(-a1_-a2... ,_-an) = f(a1a2... ,аn) = — f(la1 la2,...,1an) — g(1) и, значит, g(х) - константа; при этом мы воспользовались тем, что 0a = __а и 1а = а.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.