Высказывания. Операции дизъюнкции, конъюнкции и отрицания. Пропозициональные формулы, булевы функции и их количество. Класс монотонных функций. Полнота систем булевых функций, страница 3

Монотонность функции легко выясняется из ее истинностной таблицы непосредственно по определению 1. На языке функциональных схем монотонность означает, что усиление сигналов на некоторых входах схемы не приводит к уменьшению сигнала на выходе этой схемы.

Теорема о замкнутости класса М. Класс монотонных функций замкнут относительно суперпозиции.

Доказательство проведем на языке функциональных схем. Рассмотрим функциональную схему, составленную из монотонных элементов. Если усилить значения сигналов на некоторых входах этой схемы, то сигналы на выходах всех ее элементов не уменьшатся, поскольку они монотонны. Значит и сигнал на выходе схемы тоже не уменьшится, т.к. он является выходом одного из элементов схемы. Теорема доказана.

Лемма о немонотонной функции. Суперпозицией немонотонной функции f(x1,x2,... ,х_п) и констант 0, 1 можно получить отрицание х.

Определение 2. Конъюнкт К функции f называется простым, если из него нельзя удалением какого-либо сомножителя получить более короткий конъюнкт К' для той же функции f.

Теорема о минимальной ДНФ. Минимальная ДНФ состоит только из простых конъюнктов.

Доказательство. Пусть K₁ V K₂ V ... V К_n минимальная ДНФ функции f. Если бы, например, конъюнкт K₁ не был простым, то удалением сомножителей из него можно было бы получить простой конъюнкт К'₁. Тогда К'₁  V К₂ V ... V K_s - ДНФ функции f, имеющая меньшее число букв, что противоречит минимальности исходной ДНФ.

Определение 3. Сокраенной ДНФ функции f называется дизъюнкция всех ее простых конъюнктов.

Теорема о сокращенной ДНФ. Любая булева функция f, не равная тождественно нулю, равна своей сокращенной ДНФ.

Доказательство. Пусть Р₁, P₂,... ,Р_к все простые конъюнкты функции f. Докажем равенство f(x₁,... ,x_n) = P₁(x₁,... ,x_n) V V P₂(x₁,... ,x_n) V ... V  P_k(x₁,... ,x_n). Рассмотрим произвольный набор (a_i,... ,a_п) и разберем 2 случая.

1)f(a_i,... ,a_п) = 0, тогда все P_i(a_i,... ,a_п) = 0, т.к. они являются конъюнктами функции f. Отсюда следует, что дизъюнкция Pi(a_i,... ,a_п) по всем значениям i= 1,2,... ,к тоже равна 0 и искомое равенство верно.

2)f(a_i,... ,a_п) = 1, тогда конъюнкт К = x^a1₁ x^a2₂ x^an_n   равен 1 на этом наборе. Если конъюнкт К является простым, то он имеется среди P₁, Р₂,... ,Р_k и, следовательно, их дизъюнкция равна 1 на наборе (a_i,... ,a_п ).

§ 9. Полнота систем булевых функций

Определение 1. Система логических связок S = {a₁,..,а_т} называется полной, если любую булеву функцию f(x₁ x₂,  ,х_п) можно реализовать ПФ, составленной из переменных с использованием этих логических связок.

Полная система называется базисом, если никакая ее подсистема не является полной.

Определение 2. Функцию F, вычисляемую по формуле F{t₁,... ,t_m) - f(g₁(t₁,... ,t_m),g₂(t₁,... ,t_m),... ,g_n(t₁,... ,t_m)), называют суперпозицией функций f,g₁,g₂..g_n

Определение 3. Система БФ S — {ф₁,ф₂,... ,ф_m} называется полной, если любую булеву функцию F можно получить из функций ф₁,ф₂,... ,ф_m и функций I^k_n с помощью конечного числа суперпозиций, где I^k_n(x₁,X₂,...,,x_n) = х_k - функции проецирования.

Свойство. Если система S = {ф₁,ф₂,... ,ф_m} полна и каждая из функций ф₁,ф₂,... ,ф_m является суперпозицией функций w₁,w₂,w_n и функций I^k_n, то и S' = {w₁,w₂,...,w_n) тоже полная система.

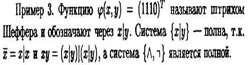
Если К не является простым, то удалением некоторых сомножителей из него получается один из простых конъюнктов, который и равен 1 на наборе (a_i,... ,a_п) и, значит, снова дизъюнкция всех простых конъюнктов равна 1.

Следствие. Минимальная ДНФ получается из сокращенной удалением некоторых простых конъюнктов (либо равна ей).

Какие именно простые конъюнкты надо удалить из сокращенной ДНФ для получения минимальной ДНФ можно узнать из таблицы истинности для простых конъюнктов (см. ниже).

§ 7. Релейно-контактные схемы