Доказательство. Первый элемент можно выбрать n способами, после этого второй элемент можно выбрать тоже nспособами и т.д., последний k-тый элемент можно выбрать также n способами. Значит последовательная выборка осуществима пк способами по принципу комбинаторного умножения. Теорема доказана.
§ 5- Отношения эквивалентности и порядка
Определение 1. Бинарное отношение Л на А называется а)рефлексивным, если Va € А ((a, а) € R);
б)симметричным, если из {х,у) € Rследует, что (у, х) € R;
в)транзитивным, если (х,у) € R, (у, z) € R => (x,z) € R;
г) антисимметричным, если (х, у) € R, (у, х) € R=> х = у.
Если бинарное отношение R на А является рефлексивным, симметричным и транзитивным, то его называют отношением эквивалентности на А и пишут х ~ у вместо (х, у) € R. Условия рефлексивности, симметричности и транзитивности можно пере- писать так а)Va € А (a~a);
б)х ~ у => у ~ х;
в)x ~ у, у ~ z => х ~z.
Если дано отношение эквивалентности на множестве A, то классом эквивалентности, порождаемым элементом х € А называется множество Кх = {у € А | у ~ x}.
Теорема о разбиении множества на классы эквивалентности. Каждое отношение эквивалентности на А порождает разбиение А на непересекающиеся классы эквивалентности.
Доказательство. Пусть Кх и Kz- классы эквивалентности. Разберем два возможных случая.
1.Пусть х ~ z. В этом случае у € Кх <=> у ~ x; поскольку х ~ z, то у ~ х <=>- у ~ z <=> у € Kz, т.е. у € Кx<=> У € Kz и значит Kx=Kz.
2.Пусть x<~> z. В этом случае КХ П Кг = 0, т.к. если бы существовал элемент у такой, что у € Кх и у € Kz, то было бы и y~ х и у ~ z => x~ z, что противоречит условию.
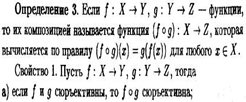

§ 2. Перестановки с повторениями
(n1,n2,..nk) -набор можно получить из данного k-множества М = {a1,a2,...,ak} размножением элемента ai,- в niэкземплярах, где ni >= 0, i— 1,2,... ,k.
Определение 1. Упорядоченный (n1,n2,..nk)-набор называется перестановкой с повторениями.
Теорема 1. Количество всех различных перестановок с повторениями (n1,n2,..nk)-набора задается формулой
![]()
Доказательство. Возьмем любую перестановку с повторениями данного набора и заменим в ней п\ экземпляров элемента а1 на разные элементы а11,а12, ... ,a1n,. Переставляя их между собой, мы получим n1! перестановок, в которых нет повторения элементов а1, но еще остались повторения элементов A2, а3, -.. , аK. Заменяя их таким же образом и переставляя между собой, получим окончательно размножение в n1!n2!n3!..nk! раз. Всего в итоге получим (n1+n2+nk)! обычных перестановок (без повторе-ний)изначит P(n1,n2,nk)*n1!n2!n3!..nk! = (n1+n2+nk)!. Отсюда следует искомая формула. Теорема доказана.


§ 3. полиномиальная формула
Теорема 1. Имеет место следующая полиномиальная
формула: ![]()
в которой индексы ![]() меняются
от 0 до n с соблюдением условия n1 + n2 + ... + nk = n.
меняются
от 0 до n с соблюдением условия n1 + n2 + ... + nk = n.
Доказательство. Левую часть полиномиальной формулы можно представить в виде произведения п скобок:
(х1+x2+-. .+xk)n =
= ((х1+x2+-. .+xk)) . ((х1+x2+-. .+xk)) ... ((х1+x2+-. .+xk)) .
После раскрытия скобок по правилу умножения многочленов, мы получим сумму одночленов степени п вида(х1n1+x2n2+-. .+xknk). Такому одночлену соответствует разбиение множества из n скобок на к подмножеств: в i-тое подмножество берем те скобки, из которых взят множитель Xi, i — 1,2,... ,n. Значит указанный одночлен встречается в количестве, равном числу разбиений множества из n скобок на kподмножеств с числом элементов n1,n2,..,nk. Согласно предыдущей задаче это количество равно Р(n1,n2,..,nk), что и завершает доказательство полиномиальной формулы.
§ 4. Сочетания и их свойства
Определение 1. Сочетанием из n по kназывается неупорядоченное к -подмножество данного n-множества.
Теорема 1. Количество всех сочетаний из п по к вычисляется
по формуле 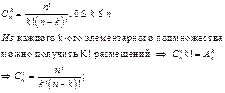
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.