Построение математической модели для предприятия, выпускающего 4 виды продукции. Решение задачи линейного программирования графическим способом

Вариант 6

Контрольная работа №1

Задание 1

Приведите к канонической форме следующую задачу линейного программирования:

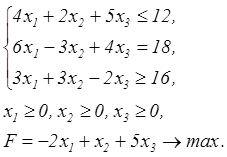
Решение:

В канонической форме задача линейного программирования является задачей максимума некоторой линейной функции , ее система ограничений состоит только из равенств, и при этом переменные задачи являются неотрицательными.

В нашем случае задана функция , которую надо максимизировать. Переменные неотрицательны. Второе ограничение является равенством. Следовательно, для преобразования данной задачи к каноническому виду, необходимо преобразовать первое и третье ограничение в равенство.

В первое неравенство введем неотрицательную переменную  со знаком «+»:

.

В третье неравенство вводим неотрицательную переменную  со знаком «-»:

.

Следовательно, данная задача в канонической форме примет вид:

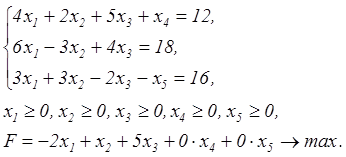
Задание 2

Постройте математическую модель

Хозяйство располагает следующими ресурсами: площадь – 100 ед., труд – 120 ед., тяга – 80 ед. Хозяйство производит четыре вида продукции: . Организация производства характеризуется следующей таблицей:

Продукция	Затраты на 1 ед. продукции			Доход от единицы продукции
	площадь	труд	тяга
	2	2	2	1
	3	1	3	4
	4	2	1	3
	5	4	1	5

Составить план выпуска продукции, обеспечивающий хозяйству максимальную прибыль.

Решение:

Обозначим через  количество единиц продукции соответственно  планируемой к выпуску, а через  - величину прибыли от реализации этой продукции. Учитывая доходы от единицы продукции, запишем величину прибыли – целевую функцию – в следующем виде:

                                                       (1)

Переменные  должны удовлетворять ограничениям, накладываемым на расход имеющихся в распоряжении хозяйства ресурсов. Для ресурса площади имеем:

.                                                 (2)

Для ресурсов труда и тяги аналогично имеем:

,                                                   (3)

.                                                      (4)

По смыслу задачи переменные не могут выражаться отрицательными числами, т.е.

                                                                    (5)

Соотношения (1) – (5) образуют экономико-математическую модель задачи.

Итак, математически задача сводится к нахождению

Итак, математически задача сводится к нахождению числовых значений  переменных , удовлетворяющим линейным неравенствам (2)-(5) и доставляющих максимум линейной функции (1).

Решим данную задачу симплекс-методом. Для этого приведем полученную задачу к канонической форме, введя дополнительные переменные :

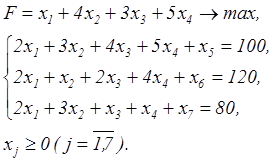                                        (6)

Запишем полученную каноническую модель (6) в виде симплекс-таблицы (таб.1):

                               Таблица 1

Т.к. в –строке таблицы 1 есть отрицательные элементы, то опорный план таб. 1 не является оптимальным. Улучшим его. Для этого выполним симплексное преобразование с разрешающим элементом – 5, который соответствует 4-му разрешающему столбцу (с минимальным элементом в  –строке) и 1-ой разрешающей строке, определенной минимальным симплекс-отношением:

.

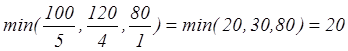В результате получим новый опорный план (таб.2).

    Таблица 2

В  – строке таблицы 2 есть отрицательные элементы, значит, опорный план таб.2 не является оптимальным. Аналогично предыдущему улучшаем его до тех пор, пока в –строке все элементы не станут положительными (таб. 3).

    Таблица 3

Т.к. в –строке таблицы 3 нет отрицательных элементов, то опорный план таб. 3

является оптимальным.

Итак, по оптимальному плану следует изготовить 25 единиц продукции  и 5 единиц продукции , продукцию  и  изготавливать не следует. При этом хозяйство получит максимальную прибыль в размере 125 ден.ед.

Задание 3

Решить задачу линейного программирования графическим способом.

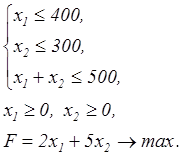
Решение:

Запишем системы граничных прямых:

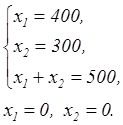                                                          (2)

На плоскости  построим граничные прямые (система (2)) и стрелками отметим те полуплоскости, множество точек которых удовлетворяют данным неравенствам (система (1)) (Рис.1).

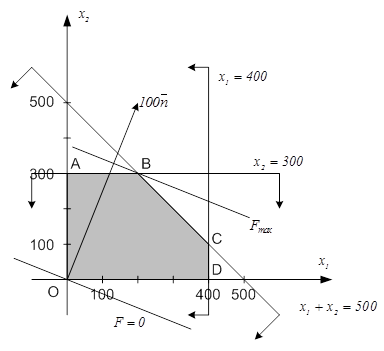
Рисунок 1

Из рисунка 1 видим, что областью допустимых решений задачи является