МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
Кафедра «Информационной безопасности»
ОТЧЕТ
по лабораторной работе:
«Построение нелинейной математической
модели для решения задачи поиска оптимального
проектного решения»
Выполнил: Яргин В.Ю.
группа ЭиП-514
Проверил: Баландин А.В.
г. Челябинск 2008
Предприятие, в состав которого входят специализированные подразделения, разрабатывает и изготавливает заданный вид продукции. При этом используются следующие факторы: сырьё, оборудование и труд. Изготовление продукции может осуществляться любым из n возможных технологическим режимом.
Необходимо по экспериментальным данным (таблица 1), используя метод наименьших квадратов, найти коэффициенты нелинейной модели.
|
№ |
|
|
|
|
|
Сырье |
Оборудование |
Труд |
Программа |
Прибыль |
|
1 |
1 |
3.842 |
1.331 |
2.441 |
2.313 |
400 |
80 |
1400 |
2000 |
60 |
|
2 |
1 |
5.772 |
1.331 |
2.441 |
2.313 |
420 |
90 |
1500 |
2010 |
70 |
|
3 |
1 |
3.842 |
2.571 |
2.441 |
2.313 |
430 |
105 |
1800 |
2030 |
65 |
|
4 |
1 |
5.772 |
2.571 |
2.441 |
2.313 |
470 |
136 |
2000 |
2000 |
80 |
|
5 |
1 |
3.842 |
1.331 |
5.062 |
2.313 |
410 |
83 |
1900 |
2050 |
66 |
|
6 |
1 |
5.772 |
1.331 |
5.062 |
2.313 |
431 |
94 |
2700 |
2060 |
80 |
|
7 |
1 |
3.842 |
2.571 |
5.062 |
2.313 |
450 |
100 |
2300 |
2040 |
76 |
|
8 |
1 |
5.772 |
2.571 |
5.062 |
2.313 |
500 |
130 |
2900 |
2090 |
90 |
|
9 |
1 |
3.842 |
1.331 |
2.441 |
4.827 |
440 |
91 |
1950 |
2060 |
70 |
|
10 |
1 |
5.772 |
1.331 |
2.441 |
4.827 |
480 |
125 |
2400 |
2070 |
85 |
|
11 |
1 |
3.842 |
2.571 |
2.441 |
4.827 |
460 |
146 |
2500 |
2050 |
80 |
|
12 |
1 |
5.772 |
2.571 |
2.441 |
4.827 |
490 |
150 |
3000 |
2080 |
95 |
|
13 |
1 |
3.842 |
1.331 |
5.062 |
4.827 |
465 |
120 |
3600 |
2060 |
80 |
|
14 |
1 |
5.772 |
1.331 |
5.062 |
4.827 |
475 |
140 |
3100 |
3000 |
96 |
|
15 |
1 |
3.842 |
2.571 |
5.062 |
4.827 |
250 |
155 |
3200 |
3100 |
90 |
|
16 |
1 |
5.772 |
2.571 |
5.062 |
4.827 |
550 |
170 |
3500 |
3300 |
100 |
В качестве аппроксимирующей зависимости возьмём степенную функцию Кобба-Дугласа n -го порядка
![]()
Точность аппроксимации проверим вычислением индекса корреляции. Индекс корреляции отображает наличие связи между экспериментальными и теоретическими значениями и рассчитывается по следующей формуле:
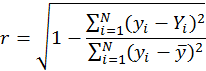
где yi— экспериментальные данные, Yi — теоретические данные, полученные при
помощи метода наименьших квадратов, ![]() — среднее значение
экспериментальных
— среднее значение
экспериментальных
данных, N — количество отсчётов.
Нахождение коэффициентов нелинейной модели для сырья
Согласно методу наименьших квадратов, сумма квадратов отклонений
теоретических данных от экспериментальных должна быть минимальной
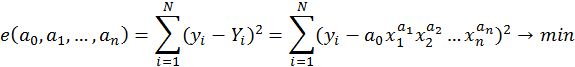
|
|
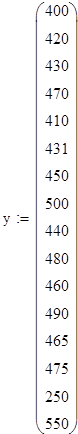
![]()
|
|
Pададим начальное приближение для коэффициентов ai и произведём
численную минимизацию функции e(a0,a1,a2,a3,a4)
|
|
|
|
|
|
|
|
|
|
|
|
В результате минимизации получено следующее решение.
|
|
|
|
|
|
|
|
|
|
Сформируем функцию для нахождения теоретических значений и посчитаем
индекс корреляции.
|
|
|
|
Индекс корреляции r =0,271 , что указывает на низкое качество аппроксимации.
Для того чтобы получить другое решение, необходимо изменить начальное приближение
для коэффициентов ai.
Изменяя начальное приближение для коэффициентов ai, добьёмся приемлемого
решения задачи аппроксимации.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, теоретические объёмы сырья, используемого при производстве
продукции, можно найти следующим образом:
![]()
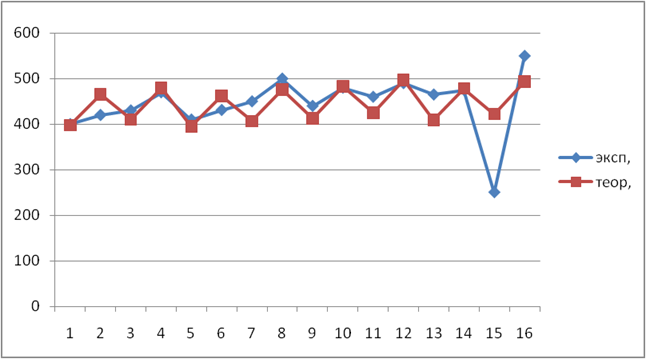
Нахождение коэффициентов нелинейной модели для оборудования
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r=0.959
![]()
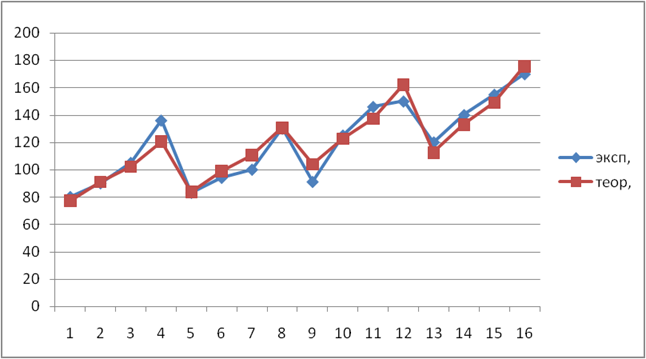
Нахождение коэффициентов нелинейной модели для труда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
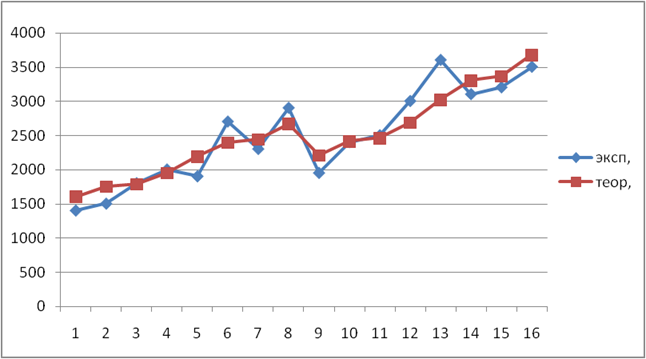
Нахождение коэффициентов нелинейной модели для программы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r=0.795
![]()
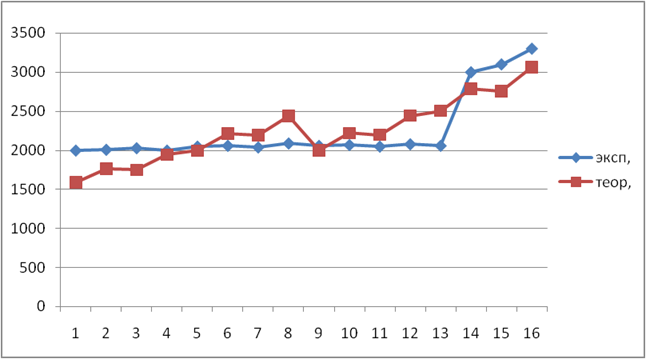
Нахождение коэффициентов нелинейной модели для прибыли
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
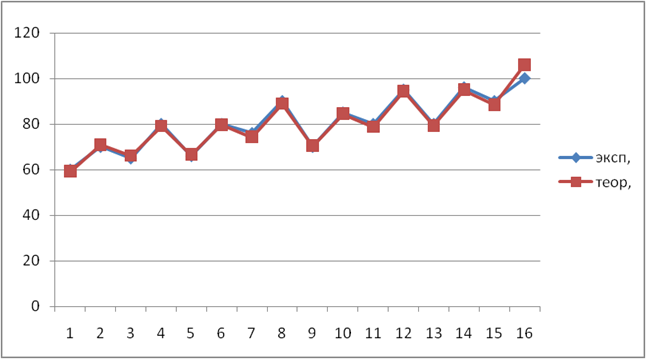
Нелинейная модель задачи оптимизации проектного решения:
![]()
При условиях:
![]()
![]() 80
80
![]()
![]() 2000
2000
![]()
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.