Техническая электродинамика: Сборник лабораторных работ (Режимы работы линий передачи. Исследование волноводных четырехплечих (гибридных) соединений), страница 7

Среднеквадратическое отклонение

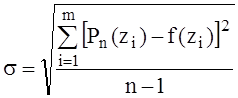
можно найти для эксперимента и теории и, сравнивая их, определить качество измерений.

Теоретически

.

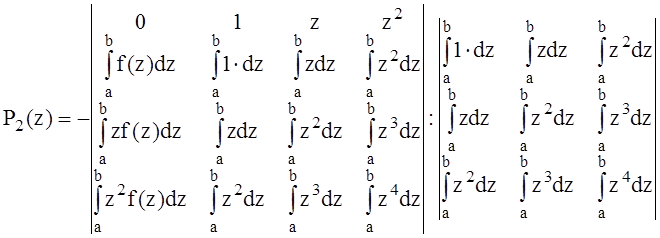В нашем случае f(z) = sin(βz); β = 2π/λ_в.

3.1. Определение положения узлов в интерференционной картине

Для повышения точности определения минимумов применяется метод «вилки». Метод «вилки» основан на симметричности интерференционной картины распределения электрической составляющей электромагнитного поля вдоль волновода относительно положения минимума. При перемещении зонда от положения минимума наибольшая чувствительность индикаторного прибора при квадратичной характеристике детектора будет в точке перегиба кривой, описывающей интерференционную картину, образованную наложением падающей на нагрузку и отражённой от неё волн. После детектирования эта зависимость описывается функцией . Точка перегиба соответствует значению .

Вблизи положений максимумов и минимумов в режиме смешанных волн чувствительность малая и, следовательно, возможна большая погрешность повторного получения выставленного ранее значения на индикаторе.

Метод «вилки» заключается в следующем. С помощью перемещения зонда вдоль линии определяется максимум показаний индикатора. Затем зонд перемещается до установления на индикаторе показаний, составляющих примерно 0,35 ¸ 0,5 от максимального. Записывается положение зонда по шкале на измерительной линии а₁. Перемещают зонд в сторону дальнейшего уменьшения показаний на индикаторе, проходят через минимум и добиваются такого же показания на индикаторе, при котором зонд находился в положении а_1, и записывают новое положение зонда а₂ .

Положение минимума определяется как

.

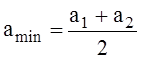На рис. 2 поясняется метод «вилки».

В режиме стоячей волны определение положения минимума также затруднено из-за наличия влияния помех вблизи нулевых значений показаний индикатора. Поэтому также применяется метод вилки.

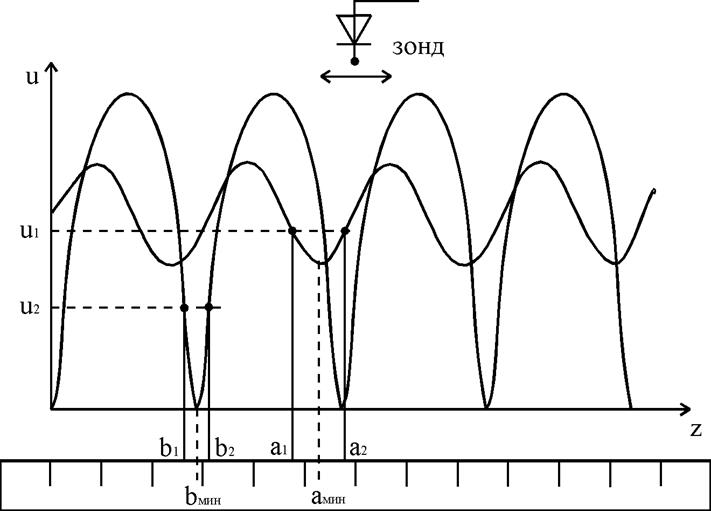
Рис. 2. Схема измерений положения минимумов в интерференционной картине в режимах смешанных волн и стоячей волны. Здесь u₁, u₂ – выбранные значения напряжения на индикаторе; а₁, а₂, b₁, b₂, – соответствующие значениям u₁, u₂ положения зонда

3.2. Измерение средних значений K_CTU

При значениях K_CTU не более трех его можно определить как отношение измеренных значений показаний индикатора в максимуме и минимуме интерференционной картине поля. При этом необходимо учитывать характеристику детектора. При выполнении точных измерений можно характеристику получить экспериментально. Большинство полупроводниковых диодов СВЧ имеют примерно квадратичную характеристику при слабых уровнях сигнала и линейную при высоких уровнях сигналов. При квадратичной характеристике детектора показания на индикаторе пропорциональны квадрату величины напряженности измеряемого электрического поля поэтому отношение

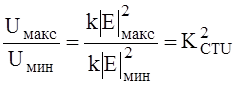,                                     (13)

где k – коэффициент передачи.

Установить вид характеристики легко по характеру интерференционной картины, построенной по результатам измерений в режиме стоячей волны. Закон изменения подчиняется зависимости , где z – расстояние от плоскости короткого замыкания.

3.3. Измерение значений K_CTU, примерно равных единице

При измерениях K_CTU @ 1 требуется особенно тщательная настройка измерительной линии. Исключить случайные погрешности измерений можно следующим способом. Снимают картину распределения поля вдоль волновода, производя большое число измерений. Затем аппроксимируют ее и строят на графике. Критерием правильности построения служит проверка расстояния между двумя минимумами, которое должно быть равно половине длины волны в волноводе. Затем определяют по графику значения максимума и минимума и рассчитывают K_CTU

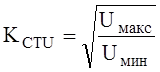.                                                (14)

3.4. Измерение больших значений K_CTU

При измерениях больших значений коэффициента стоячей волны (K_CTU > 3) отношение значений максимума и минимума на индикаторе превышает 9. Поэтому произвести отсчёт на одном пределе измерения индикатора U_макс и U_мин с одинаковой погрешностью невозможно. Коэффициент стоячей волны в этом случае вычисляют другими способами. Кроме того, вблизи нулевых показаний большую погрешность вносят различного вида помехи.