Техническая электродинамика: Сборник лабораторных работ (Режимы работы линий передачи. Исследование волноводных четырехплечих (гибридных) соединений), страница 6

Мощность в нагрузку не поступает , коэффициент отражения . В случае ,  фаза коэффициента отражения φ_н = π. В случае  фаза коэффициента отражения φ_н = 0. В случае , а  фаза коэффициента отражения , то есть зависит от величины и характера реактивной нагрузки. .

Режим смешанных волн.

Часть мощности передается в нагрузку и часть мощности не передается 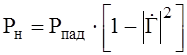. Коэффициент отражения . Фаза коэффициента отражения от нагрузки зависит от значений  и . Коэффициент стоячей волны .

Для Т-волны волновое сопротивление легко вычисляется непосредственно как отношение напряжения к току в произвольном сечении линии, работающей в режиме бегущей волны. Для других типов волн волновое сопротивление не может быть определено однозначно. Наиболее целесообразно определять волновое сопротивление через напряжение и ток. «Напряжение» определяется как интеграл от вектора  вдоль направления этого вектора, так что в случае прямоугольного волновода сечением a×b, работающего на волне Н₁₀, получаем [7, с. 146 – 149]

.

«Ток» можно определить как интеграл от вектора  вдоль границы сечения волновода; в случае прямоугольного волновода, работающего на волне Н_10, получаем

.

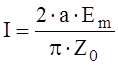Волновое сопротивление

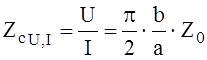, где Z₀ – характеристическое сопротивление волновода, работающего на волне Н₁₀

.

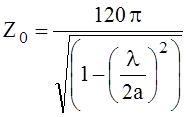Возможно также определение волнового сопротивления через напряжение и мощность

.

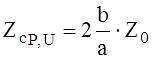Если взять для расчёта мощность и ток, то

.

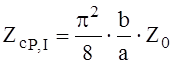В дальнейшем будем под волновым сопротивлением понимать

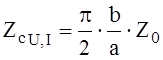, так как оно соответствует определению волнового сопротивления для Т-волны.

При рассмотрении основного типа волны Н₁₀ в прямоугольном волноводе при нормировании применяется волновое сопротивление Z_{с U,I}, по той причине, что сопротивление нагрузки представляет собой отношение напряжения к току в сечении нагрузки.

В приложениях 2 и 3 приводятся характеристики и параметры режимов работы линии передачи без учёта потерь и с учётом потерь.

3. Экспериментальное исследование режимов работы

Исследование режимов работы включает в себя снятие интерференционных картин, образованных наложением падающей и отражённой волн, вид и описание которых приводится в таблице 1 для каждого из режимов работы линии передач. Для проведения этих измерений необходимо создать в волноводе режим стоячей волны и методом вилки определить положение трёх соседних минимумов (расстояние между минимумами равно 0,5λ_в). После этого можно вычислить частоту, на которой работает генератор

.

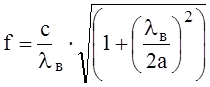Количество отсчётов, необходимых для последующего построения интерференционной картины, выбирается исходя из характера исследуемой зависимости. Для построения линейной зависимости достаточно двух точек. Для построения окружности – трёх точек. Для построения более сложных кривых количество точек увеличивается. Кроме того, для повышения точности определения кривых количество отсчётов увеличивается. Характер изменения интерференционной картины вдоль волновода синусоидальный, а из-за квадратичной характеристики детектора по результатам измерений получаем зависимость sin²βz. Поэтому для обработки и сравнения теоретических и экспериментальных зависимостей следует из полученных экспериментальных значений функции распределения извлечь квадратный корень и только затем произвести их обработку и сравнение с теоретическим законом распределения.

Одним из способов является «выравнивание» по способу наименьших квадратов [6], заключающееся в применении полиномов первой, второй, третьей и т. д. степеней для построения экспериментальной кривой по результатам измерений. Искомый полином

.

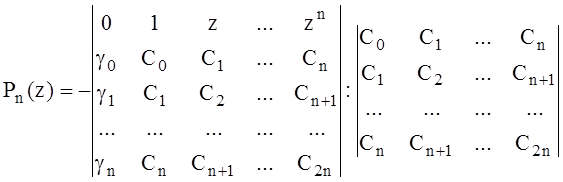Здесь 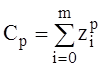  (p = 0, 1, …, 2n);  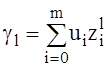 (l=0,1,…n) – коэффициенты, определяемые по результатам измерений; z_i – произведённые по шкале измерительной линии отсчёты; u_i –  показания индикатора, соответствующие отсчётам z_i после обработки, т. е. извлечения квадратного корня.

Результат – получение полинома, например

, аппроксимирующего функцию sinβz.

Можно также теоретически получить полином, аппроксимирующий исследуемую функцию и имеющий минимальное значение квадратических отклонений на исследуемом промежутке, например, для sinβz на z=λ_в/2 или λ_в/4. [6]