Техническая электродинамика: Сборник лабораторных работ (Режимы работы линий передачи. Исследование волноводных четырехплечих (гибридных) соединений), страница 5

С точки зрения технического применения линии передачи при выборе линии её свойства определяются внешними параметрами, а при её работе в конкретном устройстве – нагрузочными параметрами.

В настоящее время на основе теории длинных линий (линий с распределёнными параметрами) разработана теория СВЧ цепей [2], в которой рассматривается волновой процесс не в виде волн, определённых векторами  и , а в виде совокупности падающих и отражённых волн напряжения и тока

;

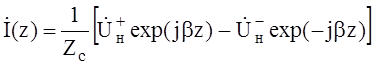,                          (1)

где ,  – комплексные амплитуды напряжения и тока в произвольном сечении линии суммы падающей и отражённой волн; , – комплексные амплитуды напряжения падающей и отражённой волн в точке подключения нагрузки (z = 0);  – фазовая постоянная;  – волновое сопротивление линии.

Мощность, поглощаемая нагрузкой

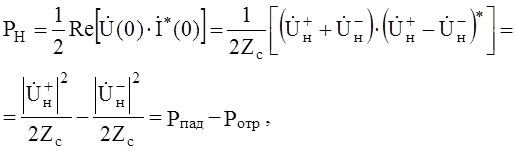                        (2)

где Р_пад – мощность, падающая на нагрузку; Р_отр – мощность, отражённая от нагрузки.

В диапазоне сверхвысоких частот удобно производить измерение мощности, поэтому удобно ввести нормированные волны, если принять

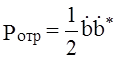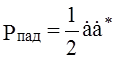, , то выражения для нормированных волн принимают вид

,                                          (3)

где  ,  ,  ,  .

Нормированные значения напряжения и тока имеют одинаковую размерность (Вт)^1/2, отличающуюся от истинной лишь постоянным множителем. Фазу нормированных значений  и  принимают соответствующей фазе поперечной составляющей вектора  в линии передачи.

Основным параметром, характеризующим режим работы линии, является коэффициент отражения.

Коэффициент отражения представляет отношение комплексной амплитуды напряжения отражённой волны к комплексной амплитуде падающей волны в произвольном сечении линии передачи

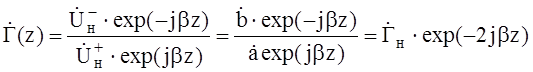,                   (4)

где 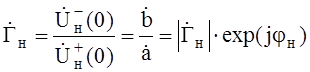 – коэффициент отражения от нагрузки;  – фаза коэффициента отражения от нагрузки.

Отношение нормированного напряжения к нормированному току в произвольном сечении линии передачи называется нормированным входным сопротивлением

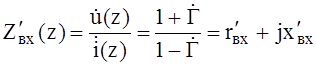,                                   (5)

где   – активная часть нормированного входного сопротивления;  – реактивная часть нормированного входного сопротивления.

Нормированное сопротивление нагрузки

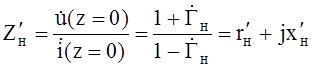.                                    (6)

Из выражений (5) и (6) легко устанавливается связь между  и

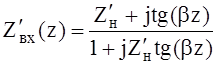.                                                (7)

Можно легко получить выражение для коэффициента отражения

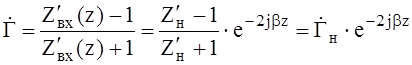.                             (8)

Передаваемая в нагрузку мощность [2]

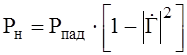, то есть зависит только от модуля коэффициента отражения. Следовательно, для определения величины передаваемой в нагрузку мощности не требуется измерения фазы коэффициента отражения, а достаточно знать модуль коэффициента отражения.

Воспользуемся выражением (3) для пояснения образования интерференционной картины наложения падающей на нагрузку и отражённой от неё волн

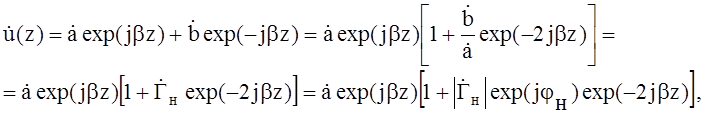 (9)

.                         (10)

Воспользуемся комплексной плоскостью для изображения поведения множителя  и построения интерференционной картины наложения падающей на нагрузку и отражённой от неё волн, показанной на рис.1. На рисунке показаны интерференционные картины наложения падающей и отражённой волны напряжения (сплошная линия) и тока (пунктирная линия).

Отношение максимального значения напряжения к минимальному в интерференционной картине называется коэффициентом стоячей волны по напряжению

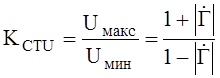.                                        (11)

Так как модуль коэффициента отражения в линии без учёта потерь равен модулю коэффициента отражения от нагрузки, то

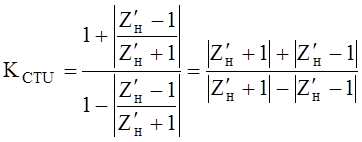,                             (12)

где  ,  .

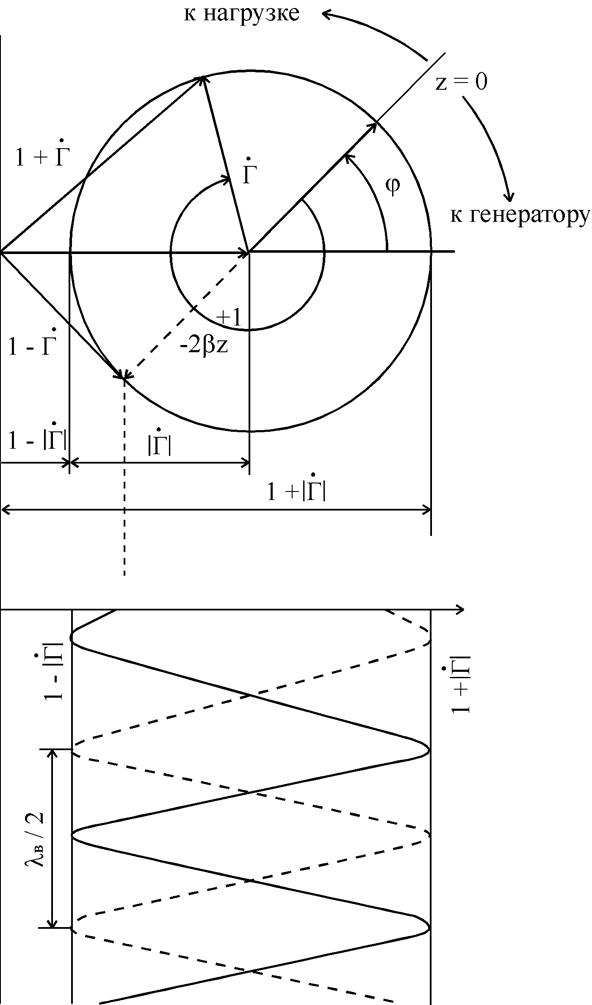
Рис.1. Образование интерференционной картины при наложении падающей

и отражённой волн

Можно сделать вывод, что величина K_CTU полностью определяется сопротивлением нагрузки, а следовательно, по величине K_CTU можно установить режим работы линии передачи.

Режим бегущей волны.

Вся мощность передается в нагрузку , то есть активная составляющая сопротивления нагрузки равна волновому сопротивлению линии передачи, а реактивная .

Коэффициент отражения , .

Режим стоячей волны.