|
Напряженное состояние |
Схема напряженного состояния |
Тензор напряжения |
Пример |
|
|
Линейное |
Основное растяжение |
|
(S)= |
Испытание гладкого цилиндрического образца на растяжение до образования шейки |
|
Одноосное сжатие |
|
(S)= |
Испытание образцов на осевое сжатие при отсутствии трения на торцах образца |
|
|
Плоское |
Двуосное растяжение |
|
(S)=
|
Изгиб широкого образца и испытание под внутренним давлением тонкостенных цилиндров |
|
Двуосное сжатие |
|
(S)= |
Кольцевое сжатие цилиндрических образцов на боковой поверхности |
|
|
Двуосное разноименное напряженное состояние |
|
(S)= |
Кручение цилиндрического стержня |
|
|
Объем |
Трехосное растяжение |
|
(S)= |
Гидростатическое сжатие в центре нагреваемого шара |
|
Трехосное сжатие |
|
(S)= |
Испытание на твердость при вдавливании индентера |
|
|
Разноименное объемное напряженное состояние |
|
S)= |
Холодное волочение металла |
|
В результате механических испытаний, в значительной степени определены схемы, которые определяются условиями нагружения.
1.1 Напряженное состояние.
Для определения напряженного состояния в какой-то точке приводится бесконечно малый параллелепипед (в теории), т. о. чтобы его ребра составляли прямоугольную систему координат.
Напряженное состояние в любой точке тела характеризуется девятью величинами: 6 касательными и 3 нормальными напряжениями и записывается как тензор напряжения.
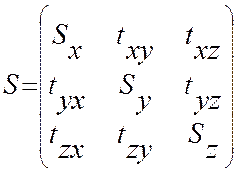 - тензор напряжения.
- тензор напряжения.
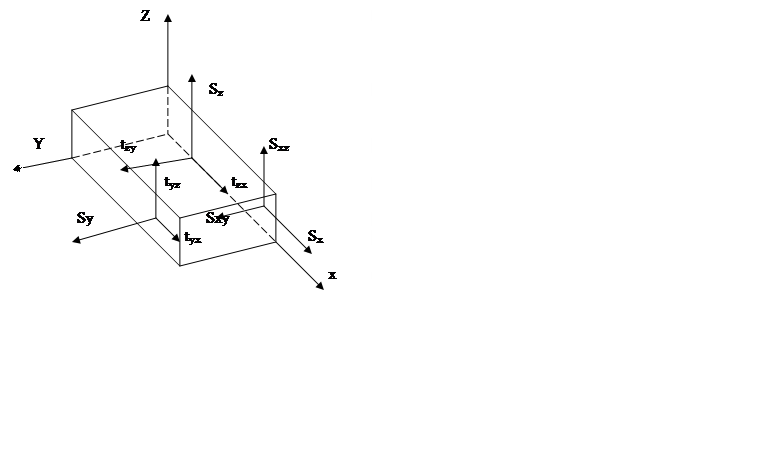
Рис.3 бесконечно малый параллелепипед.
Теория
упругости и пластической деформации доказывает, что при любом напряженном
состоянии в любой точке тела можно провести, по крайней мере 3 взаимно
перпендикулярные площадки, на которой действуют касательные напряжения и касательные
напряжения равны нулю, действительно только ![]() . Такие
площадки называют главными, а нормали к ним – главными
направлениями:
. Такие
площадки называют главными, а нормали к ним – главными
направлениями:
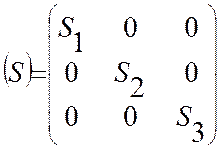 ,
где S1, S2, S3соответственно наибольшие средние и наименьшие главные
напряжения.
,
где S1, S2, S3соответственно наибольшие средние и наименьшие главные
напряжения.
(S) является также функцией, которая для любой заданной площадки, проходящей через заданною точку, определяет все напряжения, действующие в данной площадке. В реальных случаях эти площадки расположены произвольно. Для произвольной площадки, которая характеризуется углом наклона α и известны главные направления S1, S2, S3, функция
S= a2xSx+a2ySy+a2zSz
t=a2xS2x+a2yS2y+a2zS2z-( a2xS2x+a2yS2y-a2zS2z)
Т. е. cos ax, cos ay, cos az и являются направляющими произвольной площадки.
1.2 Деформационное состояние
Не при всех видах деформации происходит видимое измельчение формы и объема тела (кручение, гидростатическое сжатие). При нагрузке с деформацией (растяжение стержня) с изменением формы:
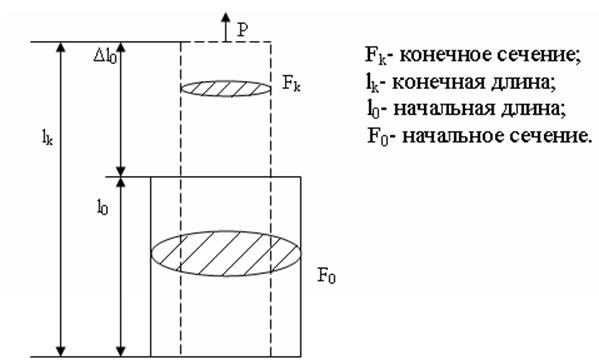
рис. 4 растяжение стержня с изменением формы.
Деформация- изменение растяжения под действием внешней нагрузки между двумя отдельными точками тела (в самом простом случае). Если деформация исчезает, после снятия напряжения у образцов восстанавливаются исходные размеры, то такую деформацию называют упругой. Если это не происходит, то деформацию называют пластической. Деформация характеризуется относительным удлинением δ:
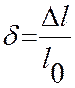
Δl- разность длин
l0- начальная длина образца
Абсолютное удлинение: Δl=lк+ l0
Δ- условная характеристика, не учитывающая изменения отношения Δl к l0.
l0,l1, l2, l3,… lk
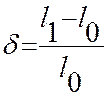 , δ1=…, …
, δ1=…, … 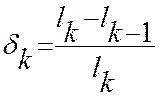
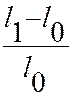 +
+ 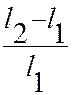 +…+
+…+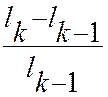 ; k
; k![]()
![]() при изменении отрезков, на которых измеряется
напряжение, до
при изменении отрезков, на которых измеряется
напряжение, до ![]() , то
получим истинное относительное удлинение:
, то
получим истинное относительное удлинение:
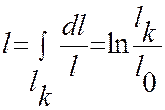
Относительное сужение ψ бывает условным и истинным.
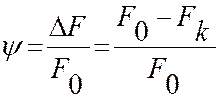 - условное
- условное
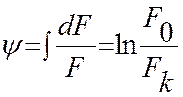 - истинное
- истинное
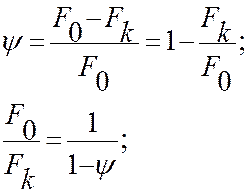
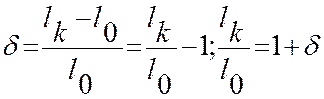 ;
;
Из этого следует закон постоянства объема:
F0l0=Fklk
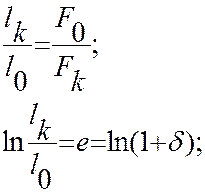
е - постоянная, которая характеризует совокупность всех смещений.
1.3 Закон Гука и константы упругости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.