Синтез планетарной передачи. Аналитический расчёт планетарной передачи

4. Синтез планетарной передачи.

       4.1.  Исходные данные:

Величина	αω, мм	Z4	Z5	m1, мм	I1H-3	m2, мм
Значение	135,0	11,0	22,0	8,0	6,5	4,0

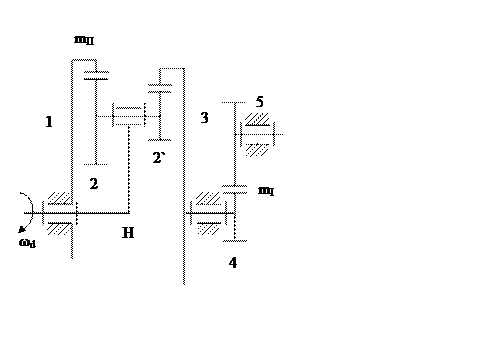
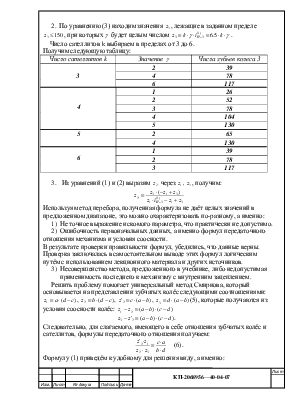
                                  Рис.1 Схема планетарной передачи

     4.2.  Аналитический расчёт планетарной передачи. 

     Синтез планетарной передачи состоит в подборе чисел зубьев колёс и числа сателлитов по заданной схеме  и передаточному отношению.

    При решении задачи используются условия соосности, сборки и соседства. Кроме того, числа зубьев колёс должны находиться в приделах от 17 до 150.

    Для подбора числа зубьев и числа сателлитов должны быть заданы схема механизмов и передаточное отношение.

1.  В соответствии с выбранной подобной схемой приведённой в учебнике записываем три уравнения и два неравенства:

уравнение заданного передаточного отношения

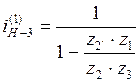                                                ,   (1)   

уравнение соосности колёс 1 и 3

                                                ,                          (2)

уравнение сборки

                                             ,                              (3)

условие соседства

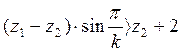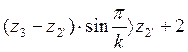                           ,  .    (4)

В уравнениях обозначено: , , ,  - числа зубьев колес 1, 2, 2`, 3

соответственно, k – число сателлитов,  - целое число.

     2.  По уравнению (3) находим значения , лежащие в заданном пределе

, при которых  будет целым числом .

    Число сателлитов k выбираем в пределах от 3 до 6.

Получим следующую таблицу:

Число сателлитов k	Значение	Числа зубьев колеса 3
3	2	39
	4	78
	6	117

4	1	26
	2	52
	3	78
	4	104
	5	130
5	2	65
	4	130
6	1	39
	2	78
	3	117

3.   Из уравнений (1) и (2) выразим  через , , получим:

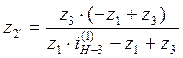
Используя метод перебора, полученная формула не даёт целых значений в предложенном диапазоне, это можно охарактеризовать по-разному, а именно:

1)  Не точное выражение искомого параметра, что практически не допустимо.

2)  Ошибочность первоначальных данных, а именно формул передаточного

отношения механизма и условия соосности.

В результате проверки правильности формул, убедились, что данные верны.

Проверка заключалась в самостоятельном выводе этих формул логическим путём с использованием лекционного материала и других источников.

3)  Несовершенство метода, предложенного в учебнике, либо недопустимая применимость последнего к механизму с внутренним зацеплением.

     Решить проблему помогает универсальный метод Смирнова, который основывается на представлении зубчатых колёс следующими соотношениями:

, , , (5), которые получаются из условия соосности колёс:

                                             .

Следовательно, для слагаемого, имеющего в себе отношения зубчатых колёс и сателлитов, формулы передаточного отношения получаем:

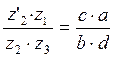    (6).

Формулу (1) приведём к удобному для решения виду, а именно:

.

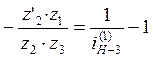Подставляя заданное передаточное отношение от водила Н – третьему колесу при неподвижном первом колесе и умножая обе части на -1, получим:

.

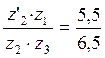Помножим число  на 10 и представим в виде сомножителей: .

И ориентируясь на соотношение (6), получим: 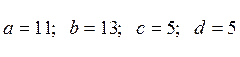, подставляя их в соотношения (5), получаем исходные числа зубьев колёс и сателлитов: 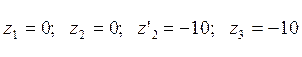(знак “-” не учитываем, берём модуль).

Полученный результат допустим, т.к. механизм будет работать в этом случае (без опорного колеса и одного сателлита). Это объясняется следующим образом: диаметры сателлита и подвижного колеса одинаковы, зацепление осуществляться будет и передаточное отношение сохраняется. Водило Н будет задавать движение (вращение) сателлита по тому же закону, что и движется сам, а сателлит в свою очередь будет вращать колесо 3.

     Комбинируя множители другим образом, получим: . Выполняя те же действия, имеем:

при 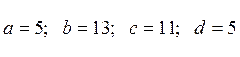, значения .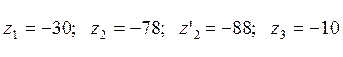

Полученные значения охарактеризуем следующим образом: такой вариант предлагает нам схему с внешним зацеплением, когда сателлит  бегает по опорному колесу 1, а  в свою очередь по подвижному колесу 3, тем самым, приводя его в движение. Передаточное отношение сохраняется, механизм работает при полученном варианте.

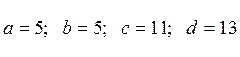    Если , то , а .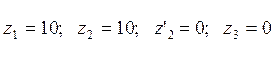

Этот вариант аналогичен первому, принцип его правильности доказывается такими же рассуждениями.

    И, наконец, при комбинации , , 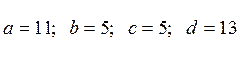следовательно, 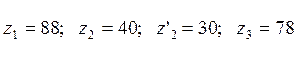. Полученные значения проверим, подставив их в формулу (1): 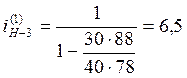. По условию , получили тождество. При изображении планетарного механизма в масштабе, используя значения последнего варианта, получаем механизм, у которого оси колёс 1 и 3 совпадают, следовательно, условие соосности выполняется. На этих основаниях можно полагать, что полученные данные – верны.

    Вариантов представления очень много, и очевидно, что при правильной компоновке все они будут верны.

    Последний вариант подходит для того, что бы использовать его в дальнейшем исследовании механизма, но на колёса 1 и 3 накладываются следующие условия:

.

Эти условия выполнены, но при ограничении  только лишь от , будет наблюдаться эффект подрезания зубьев, что вообще говоря не желательно.

Подрезания не будет в том случае, если , следовательно, колесо 3 не соответствует поставленному условию.

       Смотрим по полученной ранее таблице следующее ближайшее число зубьев колеса 3, очевидно оно равно 104, следовательно, необходимо увеличить зубья колеса 3 на 26. Для обеспечения заданного передаточного отношения, необходимо повысить число зубьев опорного колеса и сателлитов ровно во столько же раз. Это сделать невозможно при таком варианте, т.к. число зубьев колеса 3 возросло ровно на 33,333(3)%, при увеличении других колес во столько же раз, мы не сможем получить целое число зубьев. Это объясняется тем, что число зубьев 104 колеса 3 будет выполняться в том случае, если сателлитов будет 4, а в нашем случае их 2.

       Берём следующее значение равное 117. Ровно в ½ раза увеличивается число зубьев опорного колеса и сателлитов. Произведём проверку на сохранение передаточного отношения: 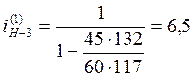, и т.к. , снова получили тождество.

       Теперь, когда все условия выполнены, можно преступить к графическому методу, но сначала, для проверки правильности решения задачи определяем передаточное отношение зубчатого механизма. Общее передаточное отношение зубчатого механизма равно произведению передаточных отношений планетарной ступени и пары зубчатых колёс 4 и 5:

.

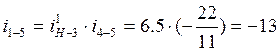Знак минус указывает на то, что водило Н и колесо 5 вращаются в противоположных направлениях.

Графическое представление рассматриваемого механизма.

Необходимо графическим методом определить передаточное отношение

Зубчатого механизма.

Алгоритм проведения графического анализа:

1)  Находим начальные диаметры колёс планетарной передачи и

вычерчиваем кинематическую схему механизма в масштабе 1:1.

2)  Строим план линейных скоростей. На вертикальную линию проецируем

все кинематические пары механизма. Т.к. движение задаёт водило Н, то из

точки о проводим под любым углом линию, до пересечения с линией bb`, тем самым задавая начальную скорость вращения. Из точки b` проводим прямую линию в точку а, лежащую на оси, получаем скорость движения сателлита 2 по опорному колесу 1. Из точки с проводим перпендикуляр на линию b`a, получаем точку c`. Из точки о проводим линию в точку c`, получаем скорость движения кинематической пары С. Т.к. скорость движения колеса 4 задаёт колесо 3, то на линию скорости колеса 3 проецируем точку е, получаем е`. Замыкаем план линейный скоростей в конечной точке f из точки е`.

3)  Строим план угловых скоростей. На продолжении линии оа откладываем

отрезок PS произвольной длины. Из точки P проводим прямые, параллельные линиям ob`, oc`, e`f, b`a, до пересечения их в точках 2, 4-5, 2`-3, Н с перпендикуляром к линии PS.

4)  Из рисунка определяем передаточное отношение планетарной передачи:

.

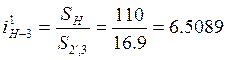Тогда общее передаточное отношение зубчатого механизма

.

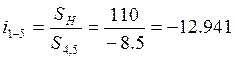Результаты построений находятся в приложении 5.

Составим таблицу полученных значений:

Передаточное                         отношение Метод	Планетарная ступень	Зубчатый механизм
Аналитически	6,5	-13
Графически	6,5089	-12,941
Отклонение, %	0,137	0,454