7. На сборку поступило десять деталей, среди которых четыре бракованные. Сборщик наудачу берет три детали. Найти вероятности событий:
A – все взятые детали стандартные;
B – только одна деталь среди взятых стандартная;
С – хотя бы одна из взятых деталей стандартная.
Решение:
Всего способов выбрать 3 детали из 10 равно ![]() .
.
Число исходов, благоприятствующих событию A равно ![]() (числу способов взять 3
стандартных детали из 4).
(числу способов взять 3
стандартных детали из 4).
p(A)= 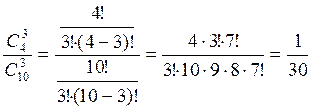 =0.033.
=0.033.
Число исходов, благоприятствующих событию B равно ![]() (числу способов взять 1
бракованную деталь из 4 умножить на число способов взять 2 стандартных детали
из 6).
(числу способов взять 1
бракованную деталь из 4 умножить на число способов взять 2 стандартных детали
из 6).
p(B)=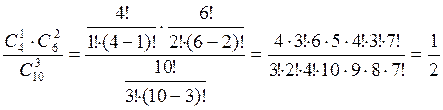 =0.5.
=0.5.
p(C)=1-p(![]() ), где
), где ![]() -
событие, при котором все взятые детали стандартные.
-
событие, при котором все взятые детали стандартные.
Число исходов, благоприятствующих событию ![]() равно
равно ![]() (числу
способов взять 3 стандартные детали из 6).
(числу
способов взять 3 стандартные детали из 6).
p(![]() )=
)=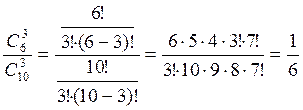 ,
,
p(C)=1-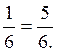 =0.83.
=0.83.
Ответ: p(A)=0.033, p(B)=0.5, p(C)=0.83.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.