ПРИМЕР РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
В качестве объекта управления рассмотрим электрическую печь сопротивления (рисунок 1). Выходная величина – температура печи, одинаковая во всех точках объема печи в установившемся состоянии θП, входная величина – сила электрического тока i, протекающего по электронагревателю с сопротивлением R. Подводимая электрическая энергия к электронагревателю расходуется на изменение температуры печи и с тепловыми потерями через кладку в окружающую среду.
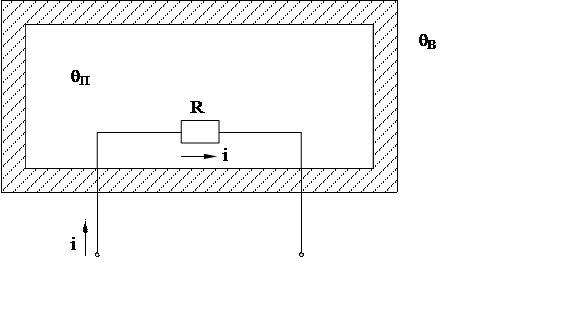 |
Рисунок 1 - Электрическая печь сопротивления
Согласно закону сохранения энергии получим уравнение динамики печи:
i2R dt=C dθП+α S (θП-θВ) dt, или i2R=C (dθП/dt)+ α S (θП-θВ), (1)
где С – теплоемкость кладки и складки печи, Дж/К;
θП и θВ – соответственно температуры печи и окружающей среды (воздуха), К;
S – площадь наружной поверхности кладки печи, м2;
α – коэффициент теплопередачи от атмосферы печи к окружающей среде, Вт/(м2К);
Полученное уравнение является нелинейным, так как входная величина-ток i имеет в уравнении вторую степень.
Установившийся в печи режим характеризуется значениями величин:
i = ![]() ; θП=θП0; θB= const.
; θП=θП0; θB= const.
Уравнение печи при этом режиме имеет вид:
![]() R=α S (θП0-θВ)
(2)
R=α S (θП0-θВ)
(2)
Разложив левую часть
уравнения печи для динамического режима в ряд Тейлора в окрестности точки i = ![]() ;θП=θП0 и оставив в этом разложении члены с ∆i = i -
;θП=θП0 и оставив в этом разложении члены с ∆i = i - ![]() в первой степени, получим уравнение вида:
в первой степени, получим уравнение вида:
![]() R+2
R+2![]() R∆i =C (dθП/dt)+ α S(θП-θВ)
(3)
R∆i =C (dθП/dt)+ α S(θП-θВ)
(3)
Вычитая из последнего выражения уравнение печи для установившегося режима (2), получаем линейное дифференциальное уравнение:
2![]() R∆i =C (dθП/dt)+ α S (θП- θП0)
(4)
R∆i =C (dθП/dt)+ α S (θП- θП0)
(4)
Введем в качестве новой выходной величины отклонение температуры печи от установившейся ∆θП=θП - θП0 и, учитывая, что θП0= const, получим линеаризованное уравнение объекта в отклонениях:
(C/(α S))(d(∆θП)/dt))+∆θП=(2![]() R/(α S))∆i (5)
R/(α S))∆i (5)
Полученное уравнение можно записать в
безразмерном виде. Для этого достаточно заменить абсолютные значения
отклонений входной и выходной величин относительными: y = ∆θП/θП0; u =
∆i/![]() .
.
Разделив обе части дифференциального уравнения (5) на θП0 , получим дифференциальное уравнение в безразмерной нормализованной форме:
(C/(α S)) (dy(t)/dt)) + y(t)=(2![]() R/(α S θП0)) u(t) (6)
R/(α S θП0)) u(t) (6)
Введем обозначения: T=C/(α S), - постоянная времени, с;
k=2i02R/(α S θП0) – коэффициент передачи (безразмерный).
С учетом введенных обозначений уравнение динамики объекта – электрической печи имеет вид:
T (dy(t)/dt) + y(t)=k u(t). (7)
Удобной формой записи дифференциальных уравнений является так называемая операторная форма, когда операция дифференцирования заменяется символом s. Тогда y(s)= W(s) u(s), где W(s) = k/(Ts+1) – оператор динамической системы.
1. Решим дифференциальное уравнение (7)
при условии, что
u(t) = u0
1(t), y(0) = 0 и t ≥ 0. После подстановки u(t) в уравнение (7) получим (u0=const):
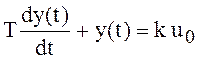 .
.
Отсутствие дельта функции в правой части свидетельствует о том, что при t = 0 величина y(t) не может измениться скачком, и следовательно, y(+0)=y(0)=0.
Характеристическое уравнение системы Ts + 1 = 0 имеет один корень 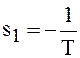 , и потому переходная составляющая решения
определяется формулой
, и потому переходная составляющая решения
определяется формулой
![]()
![]() .
.
Установившуюся составляющую следует искать в форме
правой части, то есть в виде постоянной величины ![]() .
Подставив это значение в исходное уравнение
.
Подставив это значение в исходное уравнение ![]() ,
получим (производная от константы равна нулю):
,
получим (производная от константы равна нулю): ![]() .
.
Таким образом, общее решение уравнения определяется формулой
![]() .
.
Для определения постоянной С1 следует
подставить в последнее выражение t = 0 и y(0) = 0: ![]() , откуда
, откуда ![]() . Окончательно имеем следующее выражение
для искомой реакции системы:
. Окончательно имеем следующее выражение
для искомой реакции системы:
![]() . (8)
. (8)
2. Решим дифференциальное уравнение (7) при условии, что u(t) = δ(t), y(0) = 0 и t ≥ 0. После подстановки u(t) в уравнение (7) получим:
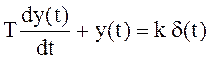 .
.
Если вместо этого уравнения рассматривать уравнение, в правой части которого отсутствует дельта-функция
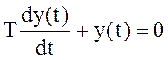 , то в качестве нового начального
значения должно быть взято значение y(+0) в момент (t = +0), непосредственно следующий за посылкой воздействия. Это
возможно так как, дельта функция существует лишь бесконечно-короткий промежуток
времени при t = 0, и ее влияние на выход может
проявиться лишь в мгновенном изменении в этот момент начальных значений
выходной величины и ее производных.
, то в качестве нового начального
значения должно быть взято значение y(+0) в момент (t = +0), непосредственно следующий за посылкой воздействия. Это
возможно так как, дельта функция существует лишь бесконечно-короткий промежуток
времени при t = 0, и ее влияние на выход может
проявиться лишь в мгновенном изменении в этот момент начальных значений
выходной величины и ее производных.
Для вычисления y(+0) проинтегрируем обе части исходного уравнения в пределах ± ε:
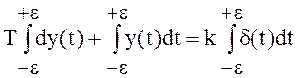 ,
,
то есть 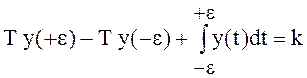 .
.
Устремив ε к нулю (осуществим предельный переход, то есть ε → 0), получим:
![]() , так как y(0)
= 0 получим
, так как y(0)
= 0 получим
![]() .
.
Рассматриваемое дифференциальное уравнение имеет общим решением
![]() .
.
После подстановки в него t =
0 и ![]() найдем
найдем ![]() .
.
Следовательно
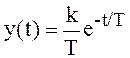 . (9)
. (9)
Уравнение (8) называется переходной характеристикой
объекта (при условии, что u0 = 1 и t ≥ 0), а уравнение (9) весовой
характеристикой. Тогда можно записать ![]() ,
, 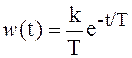 .
.
Если учитывать запаздывание объекта
τо, то при t ≥ τо 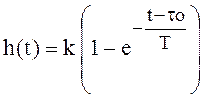 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.