





Глава 6. Некоторые нелинейные явления.
6.1. Слои в плазме.
В практических применениях плазму довольно редко можно считать бесконечной и однородной. Ее ограничивают стенки установки, электроды, поверхность зонда и т.д. Ясно, что вблизи любой ограничивающей плазму поверхности условия ее существования меняются. Оставляя в данный момент в стороне вопросы, связанные с воздействием плазмы на стенку, внесением примесей и т.д. рассмотрим ситуацию с точки зрения электростатики. Магнитное поле также исключим из рассмотрения. Представим себе вначале качественную картину. Примем потенциал плазмы равным нулю. Будем считать, что заряженные частицы, составляющие плазму, исчезают, сталкиваясь со стенкой: ионы превращаются в атомы, электроны поглощаются. При равенстве температур электронов и ионов тепловая скорость электронов существенно больше из-за малой массы и они быстрее ионов выходят на стенку, заряжая плазму положительно (или стенку – отрицательно). Поскольку вдали от стенки плазма квазинейтральна и электрическое поле в ней отсутствует, то весь перепад потенциала, вызванный указанным избытком положительных зарядов в ограниченной плазме, сосредоточится вблизи стенки, препятствуя выходу электронов так, чтобы уравнять потоки электронов и ионов на стенку. Такая пристеночная область, в которой нарушена квазинейтральность плазмы и существует градиент потенциала, называется обычно двойным слоем или слоем.
6.1.1. Задача о плоском диоде
Начнем с рассмотрения модели, которую можно представить как предельный случай слоя.
Рассмотрим плоский диод – систему, состоящую из двух бесконечных пластин 1 и 2, расположенных параллельно одна другой на расстоянии d. Одна из пластин является эмиттером заряженных частиц, ускоряемых по направлению ко второй разностью потенциалов U = j - j1. Без ограничения общности можем считать потенциал эмиттера нулевым (j1 = 0).Пусть ось x направлена перпендикулярно пластинам, плотность тока частиц, эмиттируемых с нулевыми начальными скоростями пластиной 1 равна j , масса каждой частицы m , а ее заряд q . Будем искать распределение потенциала между пластинами вдоль оси x .
Воспользуемся уравнением Пуассона, которое в данном случае будет одномерным
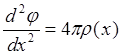 (6.1.1)
(6.1.1)
где r(x) º e×n(x) - распределение плотности заряда вдоль оси x . С учетом сохранения плотности тока вдоль x : j = e×n(x) ×v(x) = const. (v – скорость частиц вдоль оси, зависящая от пройденной разности потенциалов и, следовательно, от координаты) выразим r(x):
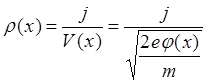 (6.1.2)
(6.1.2)
и, подставив в (6.1.1), получим
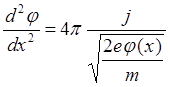 (6.1.3)
(6.1.3)
Обозначив: 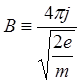 , перепишем уравнение (6.1.3) в виде:
, перепишем уравнение (6.1.3) в виде:
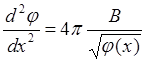 (6.1.3а)
(6.1.3а)
Первый интеграл
уравнения (6.1.3а) получим,
умножив обе его части на ![]()
![]() ,
после чего оно превратится в:
,
после чего оно превратится в:
|
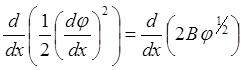 (6.1.4)
(6.1.4)
Откуда легко следует:
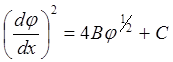 (6.1.5)
(6.1.5)
В случае 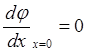 постоянная интегрирования С также
обращается в нуль, следовательно имеем:
постоянная интегрирования С также
обращается в нуль, следовательно имеем: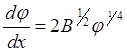 (6.1.6)
(6.1.6)
Интегрируя затем (6.1.6), получим:
|
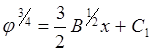 (6.1.7)
(6.1.7)
где при принятых условиях: V=0 при x=0, постоянная интегрирования также приравнивается нулю. Таким образом имеем окончательный ответ:
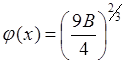 (6.1.8)
(6.1.8)
Подставляя теперь в (6.1.8) значение B, перепишем его:
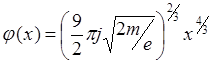 (6.1.9)
(6.1.9)
Имея в виду,
что при принятых условиях, потенциал второго электрода равен разности
потенциалов между пластинами (![]() ), выразим, используя
(6.1.9), плотность тока, проходящего через диод с расстоянием d
между электродами при разности потенциалов U между
ними:
), выразим, используя
(6.1.9), плотность тока, проходящего через диод с расстоянием d
между электродами при разности потенциалов U между
ними:
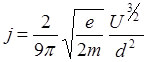 (6.1.10)
(6.1.10)
Выражение (6.1.10) называется законом Чайлда-Ленгмюра или законом «3/2».
Если U выражено в Вольтах, j – в Амперах и d – сантиметрах, то «Закон 3/2» будет выглядеть следующим образом :
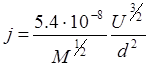
M – масса частиц в единицах протонной массы. В частности для электронов M=1/1840 и выражение примет вид
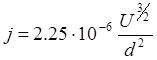
6.1.2. Плоский слой
Перейдем теперь к исследованию стационарной ситуации при которой поток холодных ионов (Ti = 0) плазмы идет на стенку вдоль оси x, ускоряясь полем слоя (которое одновременно препятствует уходу электронов). Будем считать, что в точке x = 0 скорость ионов vi = v0 и плотность n0 .
Используем, как и в предыдущем случае, одномерное уравнение Пуассона. Здесь нам придется учесть уже два сорта частиц, вносящих вклад в формирование плотности объемного заряда: ионы и электроны. Плотность ионов можно выразить с помощью следующих соображений : они ускоряются электростатическим полем при сохранении плотности потока .
Запишем для потока ионов закон сохранения энергии :
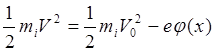 (6.1.11)
(6.1.11)
и уравнение непрерывности:
![]() (6.1.12)
(6.1.12)
Выразив затем из (6.1.11) текущую скорость ионов V(x) , получим с помощью (6.1.12) текущую плотность ионов:
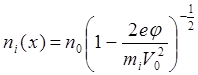 (6.1.13)
(6.1.13)
Что касается электронов, то для них примем Больцмановское распределение:
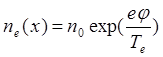 (6.1.14)
(6.1.14)
Тогда уравнение Пуассона запишется в следующем виде:
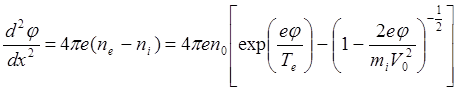 (6.1.15)
(6.1.15)
Уравнение (6.1.15) можно переписать более компактно:
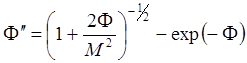 (6.1.16)
(6.1.16)
если ввести безразмерные переменные:
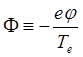 ;
; 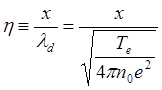 ;
; 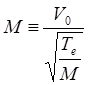 ;
; 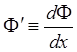 . (6.1.17)
. (6.1.17)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.