Слои в плазме. Сила высокочастотного давления, страница 2

Первое интегрирование уравнения (6.1.17) можно провести в общем виде, домножив обе его части на :

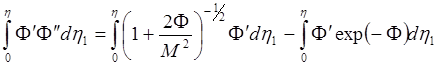        (6.1.18)

Учитывая, что при ,  (поле в плазме отсутствует), получаем:

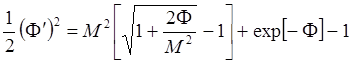                       (6.1.19)

Дальнейшее интегрирование может быть выполнено только численно, однако и не производя его можно получить важный результат, проанализировав полученное уравнение (6.1.19). Видно, что его правая часть должна быть всегда положительна. Если рассмотреть область малых  (), то, разложив ее в ряд по степеням  и ограничиваясь членом второго порядка, получим условие существования решения уравнения(6.1.19):

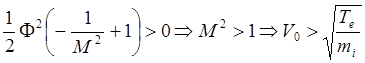                      (6.1.20)

Это неравенство называется критерием Бома, обуславливающим существование стационарного слоя в плазме. Для образования такого слоя необходимо, чтобы ионы, подходящие из плазмы к его границе, имели скорость, превышающую скорость ионного звука. Чтобы ионы в плазме могли набрать такую скорость, необходимо допустить существование электрического поля в области, предшествующей слою. Таким образом условие (6.1.20), полученное в предположении нуля поля и потенциала на границе слоя, строго говоря противоречат этим предположениям, которые могут быть теперь приняты только в качестве приблизительных. Можно предлагать различные формальные оправдания приемлемости проведенного рассмотрения от неопределенности положения границы слоя с плазмой до не вполне больцмановского распределения электронов. Физика же дела состоит в следующем: в слое плотность ионов всюду должна спадать медленнее, чем плотность электронов. При этом весь избыток положительного заряда окажется сосредоточенным вблизи стенки.

Если перейти теперь в область больших  (), то плотностью электронов можно пренебречь и уравнение (6.1.16) будет выглядеть следующим образом:

,                                         (6.1.21)

что с точностью до обозначений совпадает с использованным в предыдущем параграфе уравнением (6.1.3а), решение которого дает закон Чайлда-Ленгмюра для униполярного потока частиц в плоском диоде.

Проведенное рассмотрение дает возможность качественно описать распределение потенциала вблизи стенки состоящим из трех областей: предслоя – области в плазме с плавным нарастанием потенциала, где ионы набирают скорость, необходимую для формирования слоя – области, в которой происходит отражение основной массы электронов; размер этой области – несколько дебаевских радиусов и, наконец, области диода, размер которой определяется законом 3/2 при плотности потока ионов, определяемой скоростью рождения их в плазме. Разность потенциалов на этом диоде определяется необходимостью поддержания равенства потоков ионов и электронов на стенку.

6.1.3. Плоский зонд

Полученный критерий можно использовать для оценки ионного тока насыщения, приходящего на плоский зонд, помещенный в плазму. Площадь собирающей поверхности зонда примем равной ; на зонд подан большой отрицательный потенциал, полностью препятствующий попаданию на него плазменных электронов и собирающий все приходящие на поверхность ионы. Как следует из полученного критерия, эти ионы имеют направленную скорость

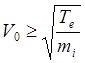                                          (6.1.22)

Тогда ионный ток на зонд определится формулой:

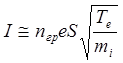                                   (6.1.23)

где n_гр – плотность плазмы у внешней границы слоя. Определим положение этой границы, как места, где скорость ионного потока в точности равна скорости ионного звука. Для достижения такой скорости ионы должны пройти разность потенциалов 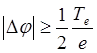, следовательно, граница слоя имеет по отношению к плазме отрицательный потенциал такой величины. Принимая электроны распределенными по Больцману, оценим их плотность в этом месте:

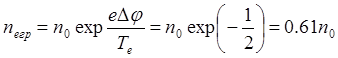                (6.1.24)

Полагая плазму квазинейтральной, перепишем соотношение (6.1.23) с учетом (6.1.24):

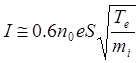                               (6.1.24)

С помощью этой формулы, измеряя ионный ток на зонд и зная температуру плазмы, можно оценить ее плотность.

6.2.      Сила высокочастотного давления.

Рассмотрим движение электрона в осциллирующих полях  и , связанных с электромагнитной волной. Постоянными полями  и  пренебрегаем. Уравнение движения электрона имеет вид:

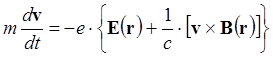                                            (6.2.1)

Пусть

                                                                   (6.2.2)

где  - пространственное распределение поля. Член  второго порядка малости и источник нелинейности.

В первом приближении им можно пренебречь. Можно также считать, что равно значению в точке (начальное положение частицы)

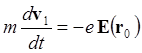                                                                     (6.2.3)

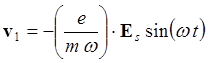                                                        (6.2.4)

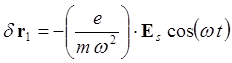                                                (6.2.5)

Анализируя величины второго порядка, нужно разложить  в ряд вблизи :

                                      (6.2.6)

В уравнении движения теперь придется учесть член , где определяется из уравнения Максвелла :

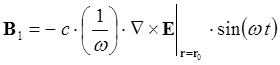                                   (6.2.7)

Часть уравнения (6.2.1), имеющую второй порядок малости, можно записать:

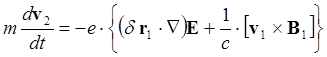                           (6.2.8)

Подставляя сюда  и  из (6.2.4) и (6.2.5) и усредняя по времени, имеем:

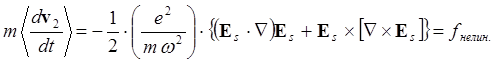          (6.2.9)

здесь использовано то, что .

Раскрываем двойное векторное произведение

и имеем из (6.2.9):

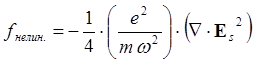                                          (6.2.10)

Это эффективное значение силы, действующей на отдельный электрон. Чтобы получить силу, действующую на 1см³, нужно умножить на плотность электронов , которую можно выразить через . Используя соотношение , имеем для силы высокочастотного давления:

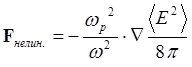                                                      (6.2.11)