Динамика жидкости. Законы сохранения и основные уравнения, описывающие движение жидкости

Лекция 10. ДИНАМИКА ЖИДКОСТИ. ЗАКОНЫ СОХРАНЕНИЯ И ОСНОВНЫЕ УРАВНЕНИЯ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ ЖИДКОСТИ.

Изучение движения жидкости как системы большого количества взаимодействующих и движущихся частиц – очень сложная задача.

Метод Лагранжа: задать для каждой частицы.

Метод Эйлера: следить не за частицами, а за отдельными точками пространства.

Состояние движения (течения) жидкости можно определить, если в каждой точке пространства, в котором она движется, известен вектор скорости проходящих частиц, как функция времени .

Общие понятия:

1. Полем векторов скорости называется совокупность мгновенных векторов скоростей, заданных для всех точек пространства, в котором движется жидкость.

2. Линией тока (рис. 1) называется линия, касательная к которой в любой точке совпадает с направлением скорости частиц жидкости в данной точке.

 

3. Стационарное (ламинарное, установившиеся) движение (течение) жидкости  поле скоростей и линии тока не изменяются с течением времени .

4. Трубкой тока (рис. 2) называется часть жидкости, ограниченная линиями тока.

 

5. Идеальной жидкостью называется  несжимаемая  и невязкая жидкость, т.е. модель реальной жидкости, деформацией которой и силами вязкого трения в которой можно пренебречь

а) Уравнение неразрывности струи для стационарного течения идеальной жидкости.

 

Пусть через S₁ запротечет масса жидкости   

                                                                                                     (1)              

За это через S₂ протечет та же масса

 

               

          Теорема                                   при стационарном (ламинарном) течении идеальной жидкости                      величина   постоянна в любом сечении

о неразрывности струи:                одной и той же трубки тока.

(1)  является выражением закона сохранения массы. Для газов (1) выполняется при скорости

б) Уравнение Бернулли для стационарного течения идеальной жидкости (рис. 3)

Рассмотрим стационарное течение идеальной жидкости в гравитационном поле.

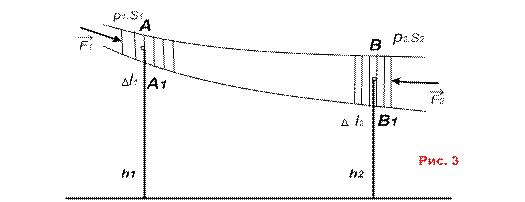Пусть за  объем жидкости АА₁ ВВ₁  переместится через сечение S₁ на , а через S₂ на расстояние .

Движение происходит под действием сил давления  и , где ,  .

При перемещении объема АА₁ ВВ₁  силы давления совершат работу: 

   (2),

где ^-  заштрихованный объем на рисунке.

Эта работа идет на изменение энергии заштрихованного объема жидкости. При перемещении АА₁ ВВ₁  за изменилась и только заштрихованного объема, следовательно:

                                                                                         

Разделим обе части этого выражение на  и перенесем в разные стороны величины, относящиеся к сечениям S₁ и S₂ :

    (3) – уравнение Бернулли        

Общий вид уравнения Бернулли :     (3`)

где   - гидростатическое давление жидкости в гравитационном поле

          -  динамическое давление движущейся жидкости.

Частные случаи:

1)  S₁=S₂, то и υ₁ = υ_2, тогда;

2)  h₁= h₂, тогда , т.е. давление больше там, где скорость меньше или площадь сечения больше.

 

в) Формула Торричелли для скорости вытекания идеальной жидкости из отверстия (рис. 4).

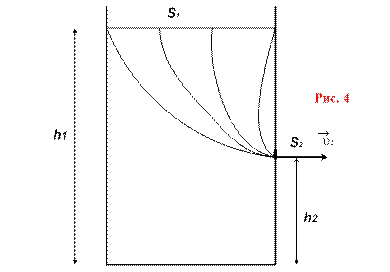
,  р₁ = р_атм = р₂

Применим уравнение Бернулли .

  (4) формула Торричелли

За dt :  (5).

Т. к. ,          (6) – сила реакции вытекающей струи = сила,  действующая на сосуд.

С учетом  (4) (7)

ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ ПО ЦИЛИНДРИЧЕСКОЙ ТРУБЕ.

 ФОРМУЛА  ПУАЗЕЙЛЯ.

Рассмотрим стационарное (ламинарное) течение несжимаемой жидкости, силами вязкого трения в которой нельзя пренебречь.

Экспериментально:   1) ,у стенок трубы равна нулю и максимальна на оси    

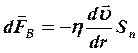                                     2)                                                                     трубы                                                                                                                                                                                                  

(8) где - коэффициент вязкости (коэффициент внутреннего трения) ~ от природы жидкости и ее температуры.

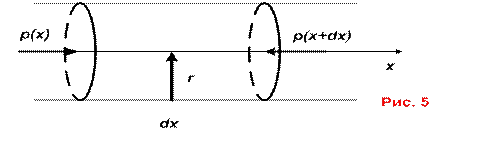Рассмотрим малую цилиндрическую трубку тока длиной dx (рис. 5). 

Модуль сил вязкого трения на боковой поверхности: . 

На  основания  этого объема

действуют силы давления, модуль результирующей которых     (9).

 

При стационарном течении , то  или .  Из (8) и (9)         (10).

Если  на dx не изменяется ,  то   (11) где р₁, р₂ – давления  на входе и выходе трубки, длина которой равна l.

С учетом (11)  (12) или   ,где С – постоянная интегрирования, которую можно найти из условия, что при r = R скорость течения равна нулю υ = 0.

Отсюда 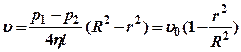    (13), где   (14) - скорость на оси (r =0)

Найдем объем жидкости, протекающий через сечение S за единицу времени (поток жидкости).

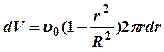  - объем, протекающий за единицу времени через сечение тонкого кольца  радиусом r.

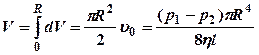  (15)- формула  Пуазейля (Объем, протекающий за единицу времени через все сечение горизонтальной трубы круглого сечения)

Согласно формуле Пуазейля, поток жидкости, при ламинарном течении, пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса трубы, но обратно пропорционален коэффициенту вязкости жидкости.