Лекция 12. ИДЕАЛЬНЫЙ ГАЗ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ (РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА).

В отсутствии внешних воздействий в газе
устанавливается равновесное состояние, при котором макропараметры:
давление р, плотность ![]() , концентрация n
и т.д. не зависят от времени и постоянны по всей системе.
, концентрация n
и т.д. не зависят от времени и постоянны по всей системе.

Если сосуд с идеальным газом находится в гравитационном
поле, то под действием силы тяжести молекулы должны располагаться в нижней
части сосуда, но, при любой температуре существует хаотическое движение. Следовательно,
давление газа р, плотность ![]() , концентрация nнепрерывно изменяются от максимального значения в нижней части сосуда до
минимального – в верхней части.
, концентрация nнепрерывно изменяются от максимального значения в нижней части сосуда до
минимального – в верхней части.
 Предположим: 1) поле тяготения однородно
Предположим: 1) поле тяготения однородно
2) t0 = const
3) mмолекул одинакова
Рассмотрим малый слой газа толщиной dh.
Разность давлений p-dp и p равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м2 (рис. 1).
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() Подставим (3) в (1)
Подставим (3) в (1)
![]() или
или ![]()
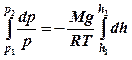 ,
, 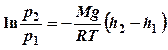 (4)
(4)

![]() (5)
(5)
 Выражение
Выражение 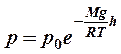 (6) называется барометрической формулой, которая
дает зависимость давления от высоты столба газа при температуре
газа Т.
(6) называется барометрической формулой, которая
дает зависимость давления от высоты столба газа при температуре
газа Т.
![]()
![]()
![]()
![]() Используем p=nkT , M=m0NA , R=kNA
(6) примет вид
Используем p=nkT , M=m0NA , R=kNA
(6) примет вид

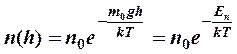 (7)
(7)
Выражение (7) - называется распределением Больцмана и показывает зависимость
![]() концентрации газа от высоты над начальным
уровнем, где Еn=m0gh –
потенциальная энергия молекулы относительно выбранного начального уровня.
концентрации газа от высоты над начальным
уровнем, где Еn=m0gh –
потенциальная энергия молекулы относительно выбранного начального уровня.

СТЕПЕНИ СВОБОДЫ МОЛЕКУЛ. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ. СРЕДНЯЯ ЭНЕРГИЯ МОЛЕКУЛЫ.
 Числом степеней свободы i называется
количество независимых величин, с помощью которых может быть задано состояние
системы.
Числом степеней свободы i называется
количество независимых величин, с помощью которых может быть задано состояние
системы.
Для характеристики энергетического состояния материальной точки в некоторый момент времени необходимо задать три координаты для определения потенциальной энергии и три проекции скорости для определения кинетической энергии, т.е. материальная точка имеет 6 степеней свободы.
![]()
Система из N материальных точек будет иметь 6N степеней свободы.
Если внешнее поле отсутствует, то число степеней свободы для линейных молекул из j атомов равно i=6j-5, а для нелинейных молекул i=6j-6 или общая формула i=6j-6(5).
Например, для линейной молекулы СО2 число степеней свободы i=6∙3-5=13, а для нелинейной молекулы H2O i=6∙3-6=12.
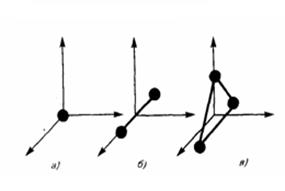
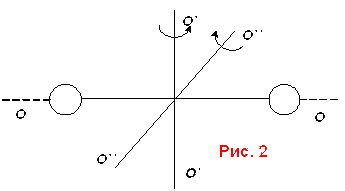 Например, модель жесткой двухатомной молекулы рассматривается
как система двух материальных точек, которые жестко связаны недеформируемой
связью, поэтому эта система имеет 5 степеней свободы.
Например, модель жесткой двухатомной молекулы рассматривается
как система двух материальных точек, которые жестко связаны недеформируемой
связью, поэтому эта система имеет 5 степеней свободы.
Какой смысл имеет это число? Центр масс молекулы может двигаться поступательно вдоль трех координатный осей, что дает 3 степени свободы для поступательного движения. Кроме того молекула может вращаться вокруг осей О`O` и O``O``, что дает 2 степени свободы для вращательного движения (рис. 2). Вращение вокруг оси ОО для материальных точек не имеет смысла
|
Модель упругой двухатомной молекулы предполагает, что атомы в молекуле связаны упругой силой, и при изменении расстояния между ними возникают колебания, что дает еще одну (колебательную) степени свободы. Для такой модели число степеней свободы 6.

Следовательно, общее число степеней свободы включает степени свободы поступательного, вращательного и колебательного движений i=in+iвр+ik.
Вращательное и колебательное движения молекул возникают при их соударениях и зависят от величины, получаемой при этом энергии.
![]() Поступательное
движение существует при всех температурах Т>0К.
Поступательное
движение существует при всех температурах Т>0К.
Вращательное движение
возникает при температурах несколько десятков Кельвин, например, для молекулярного водорода Н2
при Т![]() 86K.
86K.
Колебательное движение
возникает при высоких температурах, например, для молекулярного водорода Н2
при Т![]() 6410K.
6410K.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.