Изучение динамики вращательного движения

Белорусский государственный университет

Химический факультет

Лабораторная работа №3

«Изучение динамики вращательного движения»

Выполнили:  студентки I курса 7 группы

Кулинкина Анна Николаевна

Рогова Оксана Анатольевна

Минск 2010

Цель работы: экспериментально проверить основной закон динамики вращательного движения, определить момент инерции маятника Обербека с предельной относительной погрешностью e, не превышающей 5 %.

Оборудование и принадлежности: установка для проведения измерений, штангенциркуль.

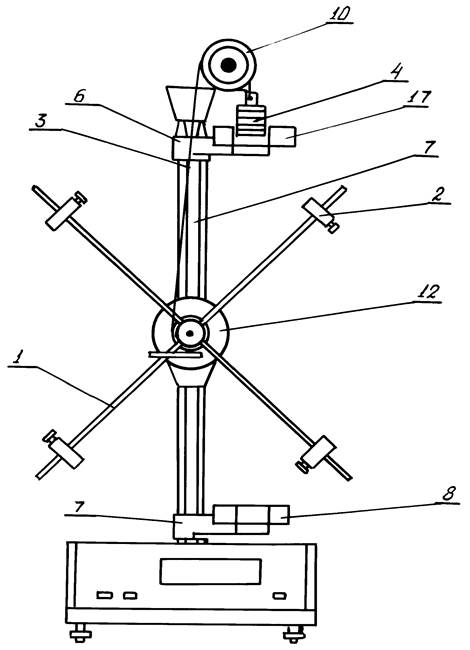
Рисунок 1

Для изучения вращательного движения используется маятник Обербека рис. 1. Он состоит из четырех взаимно перпендикулярных стержней 1, укрепленных на втулке. Втулка и два шкива различных радиусов насажены на общую ось. Ось закреплена в подшипниках, так что вся система может свободно вращаться вокруг горизонтальной оси. На стержни надеваются цилиндры 2 массой m_ц, которые могут перемещаться и закрепляться посредством винтов на любом расстоянии от оси вращения. Момент инерции маятника можно изменять, передвигая грузы вдоль стержней. На один из шкивов маятника навита тонкая нить 3, на конце которой находится груз 4 массы m. Момент силы создаваемый грузом служит для приведения маятника во вращательное движение. Груз удерживается в неподвижном состоянии с помощью фрикционной муфты, приводимой в действие электромагнитом 5. Подвижный кронштейн 6 можно перемещать вдоль колонки и фиксировать в любом положении, изменяя таким образом высоту падения груза. Для отсчета высоты на колонке нанесена шкала 7. На подвижном кронштейне 6 установлен фотоэлектрический датчик, импульсы которого служат для запуска миллисекундомера. На нижнем неподвижном кронштейне 7 закреплен фотоэлектрический датчик 8, вырабатывающий электроимпульс конца измерения времени, включающий тормозной электромагнит.

Перед началом работы необходимо с помощью регулируемых ножек основания прибора установить колонку в вертикальное положение. Установить подвижный кронштейн на выбранную высоту, чтобы грузы, падая, проходили через середину рабочего окна фотоэлектрических датчиков. При этом нижний край грузов должен совпадать с чертой на корпусе верхнего фотоэлектрического датчика.

Расчетные формулы:

                                                      (1)

где        М-момент силы;

             J-момент инерции;

            ε- угловое ускорении.

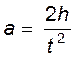                                                                                                                                        (2)

где       а- ускорение груза;

h-высота, с которой падает груз;

t-время падения.

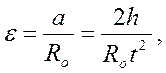                                       (3)

где- угловое ускорение;

 а- ускорение груза;

h-высота, с которой падает груз;

R₀-радиус шкива;

t-время падения.

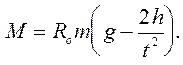                                   (4)

где       М-момент силы;

m- масса цилиндра с грузом;

g- ускорение свободного падения;

h- высота, с которой падает цилиндр;

t-время падения.

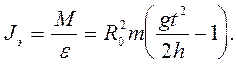                               (5)

где       М-момент силы;

- угловое ускорение;

R₀-радиус шкива;

m- масса цилиндра с грузом;

g- ускорение свободного падения;

h- высота, с которой падает цилиндр;

t-время падения.

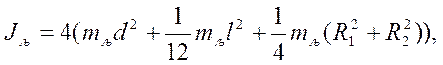                                                                                                                                           (6)

где       J_ц - момент инерции полых цилиндров относительно произвольной оси;

m_ц- масса цилиндра;

d-расстояние от оси вращения до центра масс цилиндра;

l- длина цилиндра;

R₁- внутренний радиус;

R₂-внешний радиус.

d = L + /2 + r(7)

где       d –расстояние от оси вращения до центра масс цилиндров по формуле;

L- расстояние от поверхности вала до цилиндров;

l- длина цилиндра;

r- радиус вала маятника.

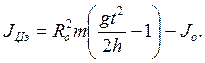                                                                                                                                          (8)

где       J_цэ –момент инерции цилиндров

R₀-радиус шкива;

m- масса цилиндра с грузом;

g- ускорение свободного падения;

h- высота, с которой падает цилиндр;

J₀ –момент инерции маятника без цилиндров.

t-время падения.

Формулы для расчета погрешностей:

(9) 

где       ε_полн. – полная относительная погрешность косвенных измерений;

ε_мин. – минимальная относительная погрешность косвенных измерений;

ε_случ. –относительная погрешность косвенных измерений.

(10) 

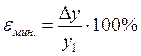
где       ε_мин. – минимальная относительная погрешность косвенных измерений;

Dy – абсолютная погрешность косвенных измерений;

y₁ –результаты первого наблюдения.

(11) 

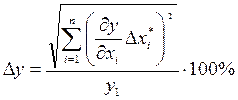
где       Dy – абсолютная погрешность косвенных измерений;

 – абсолютная погрешность прямых измерений;

y₁ – результаты первого наблюдения.

(12) 

где        – абсолютная погрешность прямых измерений;

Dx_приб. – приборная погрешность;

Dx_округ. – погрешность округлений.

(13) 

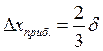
где       Dx_приб. – приборная погрешность;

δ – предельная приборная погрешность.

(14) 

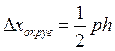
где       Dx_округ. – погрешность округлений;

p = 0,95 – доверительная вероятность;

h – интервал округления.

(15) 

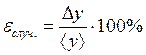
(16)   

где       ε_случ. – относительная погрешность косвенных измерений, с учётом случайной погрешности прямых мзмерений;

Dy – абсолютная погрешность косвенных измерений;

<y> – среднее значение результатов наблюдения.

(17) 

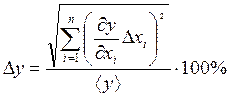
где       Dy – абсолютная погрешность косвенных измерений;

Dx_i – абсолютная погрешность прямых измерений;

<y> – среднее значение результатов наблюдения.

(18) 

где       Dx_i – абсолютная погрешность прямых измерений;

Dx_приб. – приборная погрешность;

Dx_округ. – погрешность округлений;

Dx_случ. – случайная погрешность.

(19) 

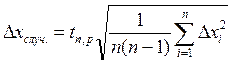
где       Dx_случ. – случайная погрешность прямых измерений;

t_n,p = 4,30 – коэффициент Стьюдента, при n=3 и p=0,95;

n – количечтво экспериментов;

Dx_i – отклонение данного результата от среднего ().

После подстановки соответствующих значений x и y получили следующие формулы для определения относительной погрешности косвенных измерений величин:

(20) 

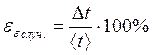
(21) 

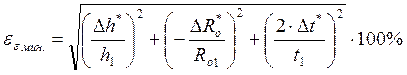
Выполнение работы

Предварительная оценка погрешностей.

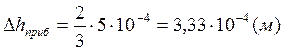
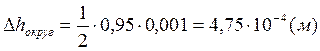
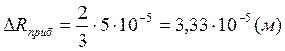
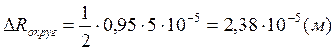
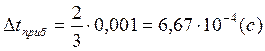
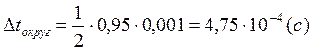
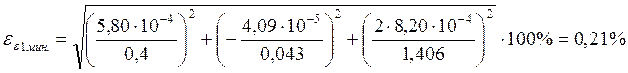
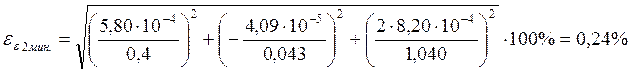
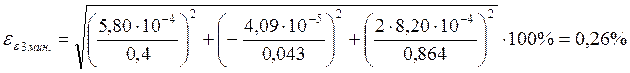
Таблица с данными, полученными в ходе эксперимента:

№ п/п	Ro м	m кг	t1 с	t2 с	t3 с	t4 с	t5 с	<t> с	h м	e с-2	M н×м	Jo кг×м2
1	0,043	0,053	1,406	1,440	1,392	1,357	1,384	1,400	0,40	9,49	0,0214	0,00226
2	0,043	0,093	1,040	1,021	1,030	1,037	1,037	1,033	0,40	17,40	0,0362	0,00208
3	0,043	0,133	0,864	0,869	0,883	0,850	0,882	0,870	0,40	24,60	0,0501	0,00204

Таблица 1

Расчёт искомых величин.

Опыт 1.1:

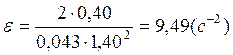
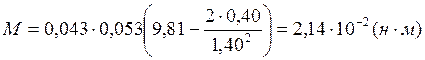
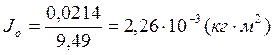
Опыт 1.2:

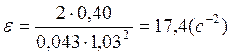
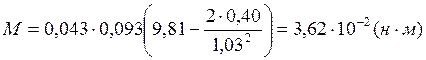
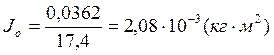
Опыт 1.3:

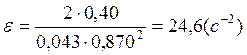
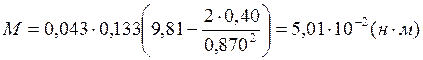
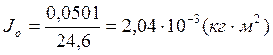
Опыт 2:

Таблица 2

№ п/п	Ro м	m кг	h м	d м	t1 с	t2 с	t3 с	<t> с	Jэ кг×м2	Jo кг×м2	Jцэ кг×м2	Jц кг×м2
1	0,043	0,053	0,400	0,223	4,403	4,343	4,383	4,376	0,0229	0,0229	0,000	0,040
2	0,043	0,093	0,400	0,223	3,296	3,274	3,297	3,289	0,0226	0,0229	3,00∙10-4	0,040
3	0,043	0,133	0,400	0,223	2,757	2,729	2,785	2,757	0,0227	0,0229	2,00∙10-4	0,040

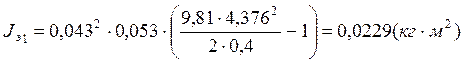
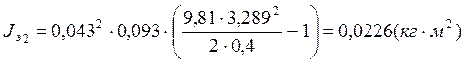
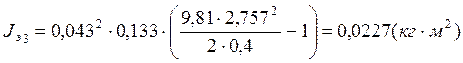
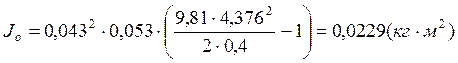
J_цэ1=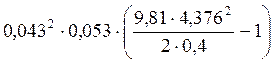-0,0229=0,000

J_цэ2=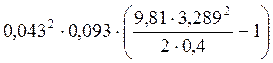-0,0229=3,00∙10^-4

J_цэ3=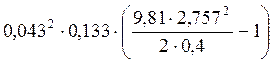-0,0229=2,00∙10^-4

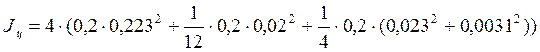=0,040(кг∙м²)

Расчёт погрешностей:

Опыт 1.1

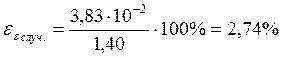
Опыт 1.2

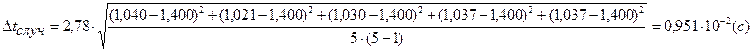
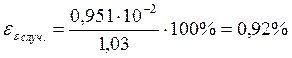
Опыт 1.3

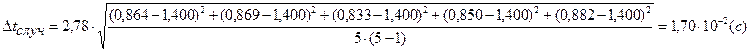
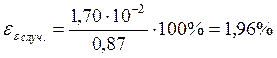
Графики:

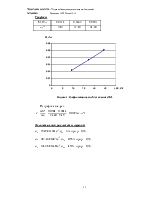
М, Н∙м	0,0214	0,0362	0,0501
ε, с-2	9,49	17,40	24,60

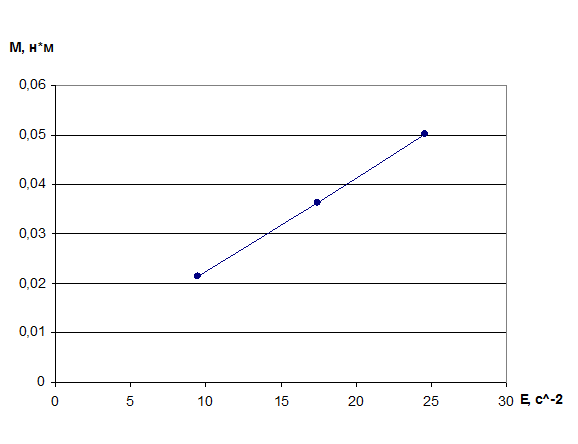
Рисунок 2. График зависимости М от ε в опыте №1.

Из графика следует:

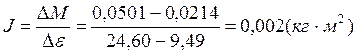
Окончательный результат измерений:

с^-2, при р = 0,95.

с^-2, при р = 0,95.

с^-2, при р = 0,95.

Вывод:

В ходе эксперимента мы опытным путем при помощи маятника Обербека проверили основной закон вращательного движения, который описывается формулой  Данное уравнение является прямым следствием законов Ньютона, поэтому его экспериментальная проверка является в то же время проверкой основных положений механики. Также оно позволяет выяснить физический смысл момента инерции: момент инерции является мерой инертности тела при вращательном движения.

В ходе первого эксперимента были рассчитанные следующие величины: ε ( угловое ускорение), М(момент сил) и J (момент инерции маятника). Результаты проведенного нами опыта, показали, что с увеличением массы груза, угловой ускорение увеличивается и момент инерции тела уменьшается. При сравнении значения J, рассчитанного по формулам, и J_о, определенного из графика, получаем