РАБОТА №2
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ КОЛЕСА
Цель работы: определить момент инерции колеса с предельной относительной погрешностью e, не превышающей 5%.
Приборы и принадлежности: колесо, платформа, набор грузов, технические весы, секундомер, штангенциркуль.
ТЕОРИЯ
Установка состоит из колеса, на вал которого накручена нить. К нити подвешена платформа для грузов. Накручивая нить на вал, поднимают платформу на некоторую высоту h1 (положение А на рисунке 1). Высота отсчитывается от положения груза при полностью раскрученной нити. Если груз отпустить, он начнет двигаться вниз под действием силы тяжести и с помощью нити приведет во вращение колесо. Когда нить полностью раскрутится (положение В), колесо, вращаясь по инерции, начнет поднимать груз. Дойдя до некоторой высоты h2 (h2< h1), груз остановится (положение С).
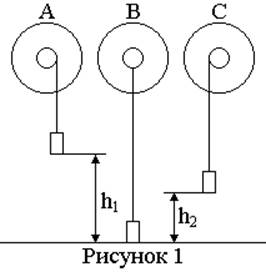
Для определения момента инерции
колеса используем закон сохранения энергии. Так как при движении системы
колесо-груз действуют неконсервативные силы (силы трения в подшипнике и силы
сопротивления воздуха), то механическая энергия системы уменьшается.
По закону сохранения энергии приращение механической энергии равно работе неконсервативных сил:
,
(1)
где Е1 и Е2 - механическая энергия системы соответственно в начальном и конечном положениях, АНК - работа неконсервативных сил при перемещении системы между этими положениями.
Применим соотношение ( l ) к перемещению системы "колесо-груз" из положения А (начальное положение) в положение В (конечное положение). Примем потенциальную энергию груза равной нулю в его нижнем положении.
Когда груз находится на высоте h1, механическая энергия системы равна потенциальной энергии груза:
, где (2)
m - масса груза с платформой.
Когда груз находится в нижнем положении, механическая энергия системы состоит из кинетической энергии груза и колеса:
,
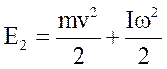(3) где v - скорость груза в нижнем положении,w - угловая скорость в этот же момент времени,
I - момент инерции колеса.
Обозначим равнодействующую всех неконсервативных сил через F. Работа этих сил при перемещении груза из верхнего в нижнее положение
. (4)
Подставив (2), (3), (4) в (I), получаем уравнение, составленное по закону сохранения энергии для рассматриваемого движения:
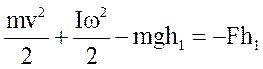. (5)
Отсюда
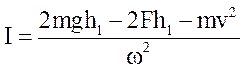. (6)
Определим v, w, t.
Так как груз движется равноускоренно без начальной скорости, то
,
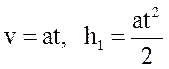(7)
где a - ускорение груза, t - время движения груза из верхнего положения в нижнее.
Из соотношений (7) получаем
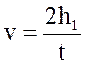. (8)
Нить, на которой подвешен груз, намотана на вал, поэтому точки, лежащие на поверхности вала, имеют линейную скорость равную скорости груза. Следовательно, v=wr, где r- радиус вала. Отсюда, используя (8), получаем
.
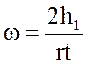(9)
Для определения F применим закон сохранения энергии (I) к перемещению системы "колесо-груз" из положения А в положение С. В положении С механическая энергия системы равна потенциальной энергии груза:
.
(10)
При перемещении системы из А в С
.
(11)
Подставим (2), (10), (11) в (1):
.
(12)
Отсюда
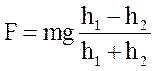. (13)
Подставим (8), (9), (13) в (6). После преобразования получим
.
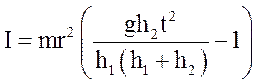(14)
ИЗМЕРЕНИЯ
1. Измерить штангенциркулем диаметр вала и определить радиус вала. Результаты занести в таблицу.
2. Определить на технических весах массу платформы и трех грузов.
3. Подвесить платформу с двумя грузами к нити и поднять их на высоту h1 (в таблицу записать положение А грузов, отсчитанное по вертикальной шкале). Отпустив груз, измерить секундомером время t его движения до нижнего положения, когда нить полностью раскрутится. Когда груз поднимется и остановится, зафиксировать положение колеса в этот момент и определить положение С по вертикальной шкале. Определить также нижнее положение В груза при полностью раскрученной нити. Все измерения положений А, В, С проводить одинаковом образом, например по низу платформы.
4. Измерения t и положений С провести 6 раз, накручивая вал 3 раза в одну сторону и 3 раза в другую. Это даст возможность скомпенсировать ошибку, связанную с возможной разбалансировкой колеса.
5. Определить h1 = В - А(
h1 берите одинаковым во всех измерениях), 
,
h2 = B - , 
.
6. Измерения п.п. 2 - 5 провести также для 2-х других грузов, массу взять большe, чем в первом случае.
7. Измерения п.п. 2 - 5 провести также для 3-х других грузов.
8. Вычислить I по формуле (14) для трех различных масс грузов.
9. Рассчитать погрешности.
10.Записать окончательный результат.
Таблица.
|
r,м |
A,м |
B,м |
h1,м |
m,кг |
t,с |
C,м |
h2,м |
I,кг×м2 |
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1.
a) Чему равен момент инерции материальной точки, тела?
b) Единица измерения момента инерции.
c) От чего зависит момент инерции тела?
d) Зависит ли момент инерции колеса в работе от массы груза? Обоснуйте ответ.
2. Чему равна механическая работа в случае:
a) постоянной силы (прямолинейное движение)?
b) переменной силы?
3. a) Что такое консервативные и неконсервативные силы? Какие неконсервативные силы действуют в работе?
b) Сформулируйте закон сохранения механической энергии.
4. Составьте уравнение по закону сохранения энергии для перехода системы колесо - груз из состояния, когда груз находится на высоте h1, в состояние, когда груз останавливается на высоте h2. Какую величину вы определяете из этого уравнения?
5. Составьте уравнение по закону сохранения энергии для перехода системы колесо - груз из состояния, когда груз находится на высоте h1 в состояние, когда нить полностью раскручена и скорость системы максимальна.
6. a) Как связаны линейная и угловая скорости ?
b) Какие точки вращающейся системы имеют линейную скорость равную скорости груза и почему?
c) Напишите основные формулы кинематики равноускоренного движения. Как они применяются в работе для вывода расчётной формулы? Почему движение груза можно считать равноускоренным?
ЛИТЕРАТУРА
1. Савельев И.В., Курс общей физики, том 1.
2. Трофимова Т.И., Курс физики.
3. Сивухин Д.В., Курс общей физики, том 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
