Лекция 6. РАБОТА. ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ.


![]()

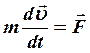 умножим на
умножим на ![]()
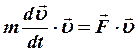
![]()


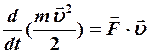 учтем
учтем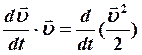 ,
,
Так как ![]() , то
, то 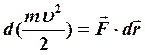 (1)
(1)

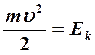 (2) - кинетическая энергия, энергия
движущегося cо скоростью
(2) - кинетическая энергия, энергия
движущегося cо скоростью ![]() тела массой m.
тела массой m.
![]()
![]() -механическая элементарная работа
(скалярная физическая величина), при
-механическая элементарная работа
(скалярная физическая величина), при ![]()
![]() (рис. 2). Работу силы можно найти
графически.
(рис. 2). Работу силы можно найти
графически.


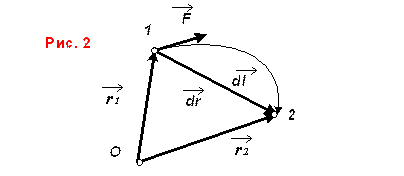
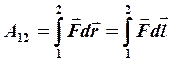 (3)
(3) 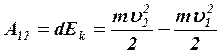 (4)
(4)

![]()
Работа сил, действующих на материальную точку, равна изменению ее кинетической энергии.

![]()
![]()
![]() Неконсервативные
(трения)
Неконсервативные
(трения) ![]()
![]()
![]() Силы
Силы
Консервативные (упругости
и тяготения)
![]()

Потенциальным полем называется область пространства, в которой действуют консервативные силы.

Математическим критерием
потенциальности поля является выражение : 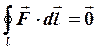 .
.
Теорема: если ![]() - консервативна,
то существует такая функция En=f(x,y,z), что:
- консервативна,
то существует такая функция En=f(x,y,z), что:



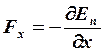 ,
, 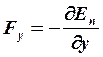 ,
, 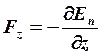 .
.
![]()
![]() Так как
Так как ![]() и
и ![]() , то
, то
 |

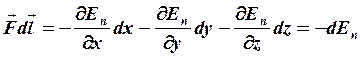 .
.

 Тогда
Тогда 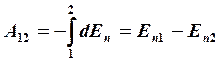 (5)
и
(5)
и ![]() . (6)
. (6)

Механической энергией называется скалярная физическая величина, характеризующая способность механической системы совершать работу.
![]()
![]()
![]() (7)-
закон сохранения механической энергии:
(7)-
закон сохранения механической энергии:

Полная механическая энергия системы в поле консервативных сил есть величина постоянная.
 Мощность. Чтобы охарактеризовать
скорость выполнения работы, вводят понятие мощности.
Мощность. Чтобы охарактеризовать
скорость выполнения работы, вводят понятие мощности. 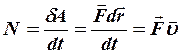 (8)
(8) ![]() =1 Вт
=1 Вт

Мощность - физическая величина, равная скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.
Закон сохранения энергии.

Энергия никогда не исчезает, и не появляется вновь, она лишь превращается из одного вида в другой.
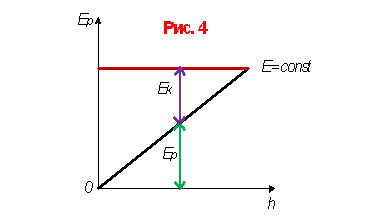
Графическое представление механической энергии.
а) потенциальная энергия тела в однородном поле силы тяжести (рис. 4).
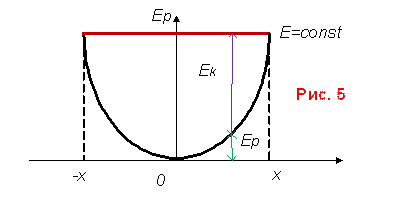
б) потенциальная энергия упругодеформированного тела (рис. 5).
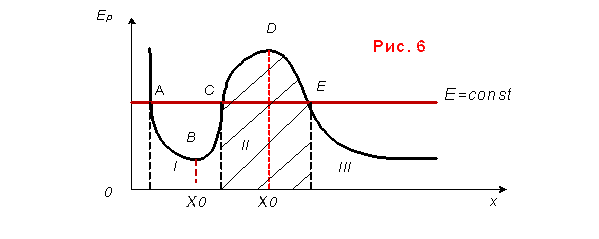
в) потенциальная кривая (рис. 6)
 |
Релятивистская механика ![]() .
.
 Основное уравнение движения
Основное уравнение движения 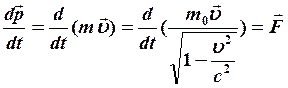 (8)
(8)
![]()
![]()
![]() можно записать
аналогично нерелятивистскому случаю
можно записать
аналогично нерелятивистскому случаю ![]() , а
после умножения на скорость:
, а
после умножения на скорость: ![]() или dA=dT ,
где
или dA=dT ,
где ![]() - релятивистская кинетическая энергия
- релятивистская кинетическая энергия
![]()
ее изменение ![]()
![]()
 Преобразуем полученное
выражение с учетом
Преобразуем полученное
выражение с учетом 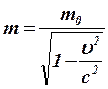 (9)
или
(9)
или ![]() .
.
![]() Найдем дифференциал от последнего
выражения
Найдем дифференциал от последнего
выражения ![]() или
или
![]()
![]() .
.
 Отсюда
Отсюда 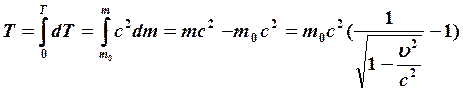 (10),
(10),

Релятивистская кинетическая энергия изменяется из-за изменения массы при разгоне тела из состояния покоя до скорости υ.
![]()
![]()
Эйнштейн: общая энергия E = mc2= m0c 2 + T (11), а при Т = 0

Е = m0c2 (12)- масса – мера энергосодержания.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.